题目内容
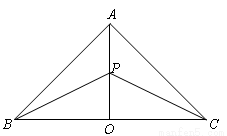
把等腰直角三角形ABC沿斜边BC上的高线AD折成一个二面角,若此时∠BAC=60°,则此二面角的大小是
90°
90°
.分析:根据平面图形翻折前后元素的变与不变,可知∠BDC即为二面角,再在△BCD中,即可求得二面角的大小.
解答: 解:如图所示:
解:如图所示:
∵等腰直角三角形ABC沿斜边BC上的高线AD折成一个二面角
∴∠BDC即为二面角
设 BD=CD=1,则 AB=AC=
∵AB=AC 且∠BAC=60°
∴△ABC为等边三角形
∴BC=
在△BCD中,∵BD=CD=1 且 BC=
,∴∠BDC=90°
即:二面角为90°
故答案为:90°
 解:如图所示:
解:如图所示:∵等腰直角三角形ABC沿斜边BC上的高线AD折成一个二面角
∴∠BDC即为二面角
设 BD=CD=1,则 AB=AC=
| 2 |
∵AB=AC 且∠BAC=60°
∴△ABC为等边三角形
∴BC=
| 2 |
在△BCD中,∵BD=CD=1 且 BC=
| 2 |
即:二面角为90°
故答案为:90°
点评:本题考查平面图形的翻折,考查面面角,解题的关键是确定面面角,搞清平面图形翻折前后元素的变与不变.

练习册系列答案
相关题目
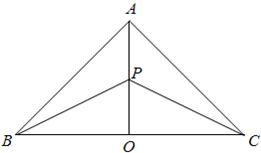 某地有三个村庄,分别位于等腰直角三角形ABC的三个顶点处,已知AB=AC=6km,现计划在BC边的高AO上一点P处建造一个变电站.记P到三个村庄的距离之和为y.
某地有三个村庄,分别位于等腰直角三角形ABC的三个顶点处,已知AB=AC=6km,现计划在BC边的高AO上一点P处建造一个变电站.记P到三个村庄的距离之和为y.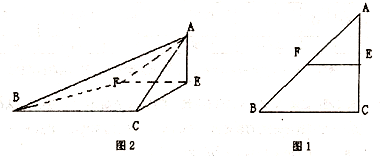 已知△ABC是腰长为2的等腰直角三角形(如图1),∠BCA=90°,在边AC、AB上分别取点E、F、,使得EF∥BC,把△AEF沿直线EF折起,使∠AEC=90°,得四棱锥A-ECBF(如图2).在四棱锥A-ECBF中,
已知△ABC是腰长为2的等腰直角三角形(如图1),∠BCA=90°,在边AC、AB上分别取点E、F、,使得EF∥BC,把△AEF沿直线EF折起,使∠AEC=90°,得四棱锥A-ECBF(如图2).在四棱锥A-ECBF中,
 ,把y表示成
,把y表示成 的函数关系式;(2)变电站建于何处时,它到三个小区的距离之和最小?
的函数关系式;(2)变电站建于何处时,它到三个小区的距离之和最小?