Question

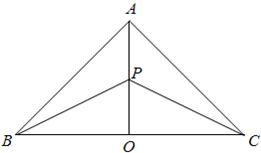某地有三个村庄，分别位于等腰直角三角形ABC的三个顶点处，已知AB=AC=6km，现计划在BC边的高AO上一点P处建造一个变电站．记P到三个村庄的距离之和为y．
（1）设∠PBO=α，把y表示成α的函数关系式；
（2）变电站建于何处时，它到三个小区的距离之和最小？

Answer 1

分析：（1）解实际应用题的关键是读懂题意，根据所给的条件知在三角形中表示出点到三个村庄的距离，表示出函数y的关系式．
（2）由题意知本题是一个求函数最小值的问题，这种类型的函数唯一的处理方式是通过导数来解题，对函数式求导，令导函数等于零，验证导函数等于零的左右两边导数的符合，得到最小值．

解答：解：（1）∵在Rt△AOB中，AB=6，
∴OB=OA=3

2

．
∴∠ABC=

π

4

由题意知0≤α≤

π

4

．
∴点P到A、B、C的距离之和为
y=2PB+PA=2×

3 2

cosα

+(3

2

-3

2

tanα)=3

2

+3

2

×

2-sinα

cosα

．
∴所求函数关系式为y=3

2

+3

2

×

2-sinα

cosα

(0≤α≤

π

4

)．

（2）由（1）得y′=3

2

×

2sinα-1

cos2α

，
令y′=0即sinα=

1

2

，
又0≤α≤

π

4

，从而α=

π

6

当0≤α＜

π

6

时，y′＜0；当

π

6

＜α≤

π

4

时，y′＞0．
∴当α=

π

6

时，y=3

2

+3

2

×

2-sinα

cosα

取得最小值，
此时OP=3

2

tan

π

6

=

6

（km），即点P在OA上距O点

6

km处．
即变电站建于距O点

6

km处时，它到三个小区的距离之和最小．

点评：本题是一个三角函数同函数结合的问题，解题过程中用到三角函数和函数的思想，是一个中档题目，高考时出上此题，不易得分，解题的关键是运算，要过运算这一关．