题目内容
本小题满分10分)已知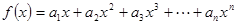 ,且
,且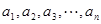 组成等差数列(
组成等差数列(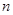 为正偶数),又
为正偶数),又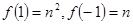 ;
;
(1)求数列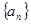 的通项
的通项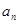 ;
;
(2)求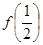 的值;
的值;
(3) 比较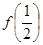 的值与
的值与 的大小,并说明理由.
的大小,并说明理由.
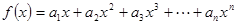 ,且
,且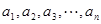 组成等差数列(
组成等差数列(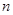 为正偶数),又
为正偶数),又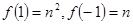 ;
;(1)求数列
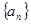 的通项
的通项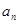 ;
;(2)求
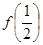 的值;
的值;(3) 比较
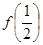 的值与
的值与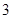 的大小,并说明理由.
的大小,并说明理由.解:(1)设数列的公差为d,
因为f(1)= a1+a2+a3+…+an=n2,则na1+
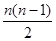 d=n2,即2a1+(n-1)d=2n.
d=n2,即2a1+(n-1)d=2n.又f(-1)= -a1+a2-a3+…-an-1+an=n,即
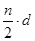 =n,d=2.解得a1="1." -------------3分
=n,d=2.解得a1="1." -------------3分∴an="1+2(n-1)=2n-1." --------------5分
(2)
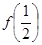 =
=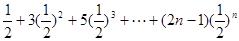 ,把它两边都乘以
,把它两边都乘以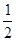 ,得:
,得: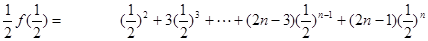
两式相减,得:
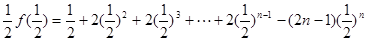
=
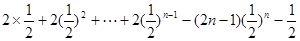 ----------7分
----------7分=
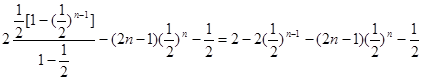
=
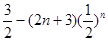 -------------10分
-------------10分(3)
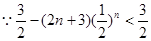
∴
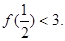 --------------12分
--------------12分略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
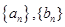 的前
的前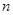 项和分别为
项和分别为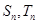 ,如果
,如果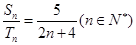 ,则
,则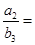 ____________.
____________.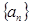 的公差
的公差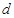 大于
大于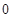 ,且
,且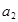 、
、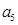 是方程
是方程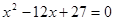 的两根.数列
的两根.数列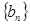 的前
的前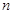 项和为
项和为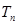 ,满足
,满足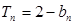
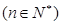

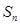 ,记
,记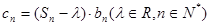 .若
.若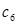 为数列
为数列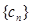 中的最大项,求实数
中的最大项,求实数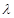 的取值范围.
的取值范围. 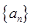 中,
中,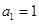 ,前
,前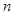 项和
项和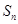 满足条件
满足条件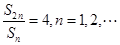 ,
, 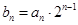 ,求数列
,求数列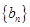 的前
的前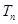

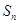 为等差数列
为等差数列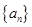 的前
的前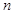 项和,若
项和,若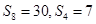 ,则
,则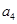 的值等于( )
的值等于( )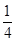
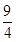
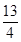
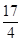
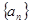 的前n项和
的前n项和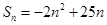 ,则关于
,则关于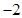 的等差数列
的等差数列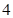 的等差数列
的等差数列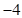 的等差数列
的等差数列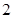 的等差数列
的等差数列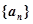 的前n项和为Sn,且
的前n项和为Sn,且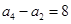 ,
,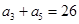 .记
.记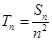 ,如果存在正整数M,使得对一切正整数n,
,如果存在正整数M,使得对一切正整数n,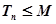
 都成立.则M的最小值是
都成立.则M的最小值是 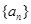 满足
满足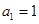 ,且
,且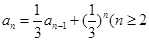 ,且
,且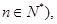 则数列
则数列