题目内容
(本题满分12分)已知圆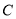 的圆心在坐标原点,且与直线
的圆心在坐标原点,且与直线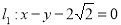 相切
相切
(1)求直线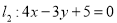 被圆
被圆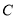 所截得的弦
所截得的弦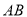 的长.
的长.
(2)过点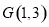 作两条与圆
作两条与圆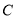 相切的直线,切点分别为
相切的直线,切点分别为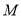 ,
,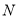 ,求直线
,求直线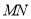 的方程
的方程
(3)若与直线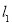 垂直的直线
垂直的直线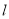 与圆
与圆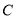 交于不同的两点
交于不同的两点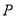 ,
,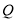 ,且
,且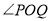 为钝角,求直线
为钝角,求直线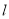 纵截距的取值范围.
纵截距的取值范围.
(1)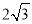 ;(2)
;(2)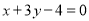 ;(3)
;(3)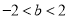 且
且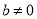 .
.
【解析】
试题分析:(1)直线与圆位置关系问题常利用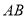 半弦长、圆
半弦长、圆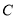 半径和圆心
半径和圆心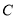 与直线
与直线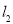 距离的直角三角关系求解;(2)先求点
距离的直角三角关系求解;(2)先求点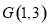 与圆心
与圆心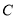 为直径的圆的方程然后与圆
为直径的圆的方程然后与圆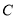 方程联立即可求得;(3)求与已知直线
方程联立即可求得;(3)求与已知直线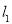 垂直直线可利用点斜式设出
垂直直线可利用点斜式设出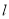 方程,让后求解
方程,让后求解
试题解析:(1)由题意得,圆心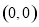 到直线
到直线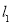 :
: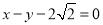 的距离即为圆的半径
的距离即为圆的半径 ,所以圆
,所以圆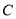 的标准方程
的标准方程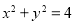 ①
①
又圆心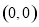 到直线
到直线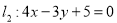 的距离
的距离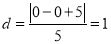 ,
,
所以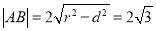 ;
;
(2)因为点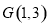 ,所以
,所以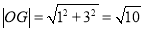 ,
,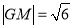
所以以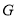 为圆心,线段
为圆心,线段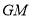 长为半径的圆
长为半径的圆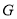 方程:
方程: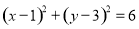 ②
②
由②-①得直线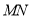 的方程:
的方程: 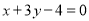 ;
;
(3)设直线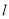 的方程为:
的方程为: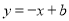 ,
,
因为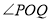 为钝角,所以所以圆心到直线
为钝角,所以所以圆心到直线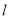 的距离
的距离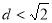 ,即
,即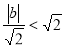 ,
,
得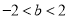 ,
,
当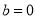 时,不满足题意,
时,不满足题意,
所以直线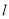 纵截距的取值范围是
纵截距的取值范围是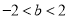 且
且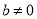 .
.
考点:直线与圆的位置关系、圆的方程、直线方程.
考点分析: 考点1:直线和圆的位置关系 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
(本题满分6分)某校高二年级的一次数学考试中,为了分析学生的得分情况,随机抽取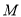 名同学的成绩,数据的分组统计表如下:
名同学的成绩,数据的分组统计表如下:
分组 | 频数 | 频率 | 频率/组距 |
(40,50] | 2 | 0.02 | 0.002 |
(50,60] | 4 | 0.04 | 0.004 |
(60,70] | 11 | 0.11 | 0.011 |
(70,80] | 38 | 0.38 | 0.038 |
(80,90] |
|
|
|
(90,100] | 11 | 0.11 | 0.011 |
合计 |
|
|
|
(1)求出表中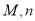 的值;
的值;
(2)为了了解某些同学在数学学习中存在的问题,现从样本中分数在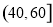 中的6位同学中任意抽取2人进行调查,求分数在
中的6位同学中任意抽取2人进行调查,求分数在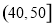 和
和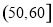 中各有一人的概率.
中各有一人的概率.
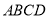 中,点
中,点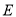 为边
为边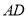 上的点,点
上的点,点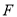 为边
为边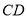 的中点,
的中点, 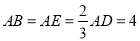 ,现将
,现将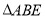 沿
沿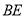 边折至
边折至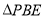 位置,且平面
位置,且平面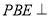 平面
平面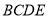 .
.
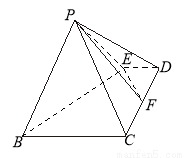
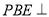 平面
平面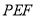 ;
;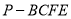 的体积.
的体积.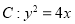 与直线
与直线 交于
交于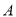 ,
,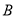 两点.
两点.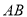 的长度;
的长度;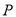 在抛物线
在抛物线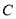 上,且
上,且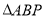 的面积为
的面积为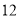 ,求
,求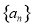 是等比数列,
是等比数列,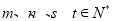 ,则“
,则“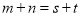 ”是“
”是“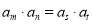 ”的( )
”的( ) 上一点
上一点 到焦点的距离为
到焦点的距离为 ,那么
,那么 的横坐标是( )
的横坐标是( ) B.
B. C.
C. D.
D.
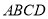 ,以下说法中,正确的序号为 (多选、少选、选错均不得分).
,以下说法中,正确的序号为 (多选、少选、选错均不得分).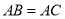 ,
,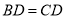 ,
,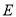 为
为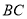 中点,则平面
中点,则平面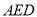 ⊥平面
⊥平面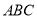 ;
;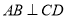 ,
,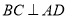 ,则
,则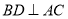 ;
;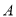 为端点的三条棱所在直线两两垂直,则
为端点的三条棱所在直线两两垂直,则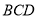 内的射影为
内的射影为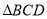 的垂心;
的垂心;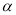 ,
,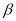 ,
,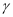 ,且
,且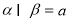 ,
,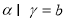 ,
,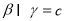 ,给出下列命题:①
,给出下列命题:①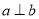 ,
,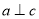 ,则
,则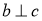 ;
;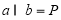 ,则
,则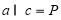 ;
;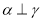 ;
;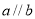 ,则
,则 。
。 的单调递减区间为 .
的单调递减区间为 .




