题目内容
对于四面体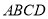 ,以下说法中,正确的序号为 (多选、少选、选错均不得分).
,以下说法中,正确的序号为 (多选、少选、选错均不得分).
①若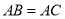 ,
,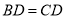 ,
,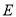 为
为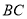 中点,则平面
中点,则平面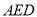 ⊥平面
⊥平面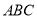 ;
;
②若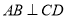 ,
,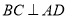 ,则
,则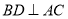 ;
;
③若所有棱长都相等,则该四面体的外接球与内切球的半径之比为2:1;
④若以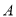 为端点的三条棱所在直线两两垂直,则
为端点的三条棱所在直线两两垂直,则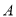 在平面
在平面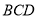 内的射影为
内的射影为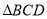 的垂心;
的垂心;
⑤分别作两组相对棱中点的连线,则所得的两条直线异面。
①②④
【解析】
试题分析:对于①,如下图所示四面体 ,
,

若 ,
, ,
, 为
为 中点,则
中点,则 ,
, ,所以
,所以 平面
平面 ,则平面
,则平面 平面
平面 ,故①正确;
,故①正确;
对于②,如下图所示,过 作
作 垂直平面
垂直平面 交于点
交于点 ,连接
,连接 ,
, ,
, 并延长分别与
并延长分别与 ,
, ,
, 交于点
交于点 ,
, ,
, ,
,

若 ,则易得
,则易得 ,若
,若 ,则易得
,则易得 ,从而可得
,从而可得 为底面
为底面 的垂心,故
的垂心,故 ,又
,又 ,所以
,所以 平面
平面 ,故
,故 ,所以②正确;
,所以②正确;
对于③,如下如图③所示,取 中点
中点 ,连接
,连接 ,设
,设 为
为 重心,连接
重心,连接 ,设
,设 上一点
上一点 为所有棱长都相等四面体的外接球与内切球的球心,外接球与内切球半径分别为
为所有棱长都相等四面体的外接球与内切球的球心,外接球与内切球半径分别为 ,
, ,那么
,那么

依题设棱长为 ,则
,则 ,
, ,
, ,在
,在 中,
中, ,
, ,
,  ,又
,又 ,即
,即 ,∴
,∴  ,
, ,故该四面体的外接球与内切球的半径之比为3:1,即③错误;
,故该四面体的外接球与内切球的半径之比为3:1,即③错误;
对于④,由②证明过程易知④正确;
对于⑤,如下图⑤所示, ,
, ,
, ,
, 分别为
分别为 ,
, ,
, ,
, 中点,连接
中点,连接 ,
, ,
,

易得 ,
, ,即
,即 ,∴
,∴  ,
, ,
, ,
, 四点共面,即棱中点连线
四点共面,即棱中点连线 ,
, 共面, 故⑤错误;
共面, 故⑤错误;
考点:立体几何点线面位置关系、平行、垂直关系判断
考点分析: 考点1:点、线、面之间的位置关系 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
 上与其焦点的距离等于
上与其焦点的距离等于 的点的坐标是 ;
的点的坐标是 ; ,使得
,使得 成立”为假命题,则实数
成立”为假命题,则实数 的取值范围是________
的取值范围是________ 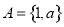 ,
, ,则“
,则“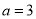 ”是“
”是“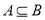 ”的( )
”的( ) 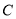 的圆心在坐标原点,且与直线
的圆心在坐标原点,且与直线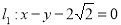 相切
相切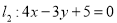 被圆
被圆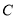 所截得的弦
所截得的弦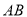 的长.
的长.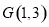 作两条与圆
作两条与圆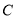 相切的直线,切点分别为
相切的直线,切点分别为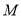 ,
,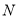 ,求直线
,求直线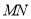 的方程
的方程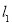 垂直的直线
垂直的直线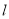 与圆
与圆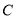 交于不同的两点
交于不同的两点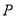 ,
,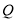 ,且
,且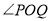 为钝角,求直线
为钝角,求直线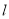 纵截距的取值范围.
纵截距的取值范围. ,其中
,其中 ,若动直线
,若动直线 与函数
与函数 的图像有三个不同的交点,它们的横坐标分别为
的图像有三个不同的交点,它们的横坐标分别为 、
、 、
、 ,则
,则 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
 的反函数为
的反函数为



 在区间
在区间 上递减,则实数
上递减,则实数 的取值范围是
的取值范围是 B.
B. C.
C. D.
D.
 ,则Z的模等于 。
,则Z的模等于 。