题目内容
19．给出如图的一个算法的程序框图，则输出S的值是（ ）
| A． | 15 | B． | 31 | C． | 63 | D． | 32 |
分析 分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可得该程序的作用是利用循环计算并输出S值．模拟程序的运行过程，对程序运行过程中各变量的值进行分析，即可得到最终的输出结果．
解答 解：第一次循环，i=1＜4，S=1+2=3，i=2，
第二次循环，i=2＜3，S=3+4=7，i=3，
第三次循环，i=3＜4，S=7+6=13，i=4，
第四次循环，i=4，S=13+8=21，不符合判断条件，输出S=21．
故选B．
点评 据流程图（或伪代码）写程序的运行结果，是算法这一模块最重要的题型，其处理方法是：①分析流程图（或伪代码），从流程图（或伪代码）中既要分析出计算的类型，又要分析出参与计算的数据（如果参与运算的数据比较多，也可使用表格对数据进行分析管理）；②建立数学模型，根据第一步分析的结果，选择恰当的数学模型；③解模型．属于基础题．
练习册系列答案
期末集结号系列答案
相关题目
9．
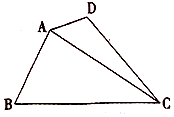如图，四边形ABCD中，∠BAD=135°，∠ADC=120°，∠BCD=45°，∠ABC=60°，BC=$\sqrt{3}$，则线段AC长度的取值范围是（ ）
如图，四边形ABCD中，∠BAD=135°，∠ADC=120°，∠BCD=45°，∠ABC=60°，BC=$\sqrt{3}$，则线段AC长度的取值范围是（ ）| A． | $[{\sqrt{2}，\sqrt{3}}）$ | B． | $[{\frac{3}{2}，\sqrt{3}}）$ | C． | $（{\sqrt{2}，\sqrt{3}}）$ | D． | $（{\frac{3}{2}，\sqrt{3}}）$ |
7．下列程序语句不正确的是（ ）
| A． | INPUT“MATH=”；a | B． | PRINT“MATH=”；a+b+c | ||
| C． | y=b-c | D． | a+b=c |
14．已知双曲线$\frac{x^2}{16}-\frac{y^2}{9}$=1的左、右焦点分别为F1，F2，若双曲线上一点P满足∠F1PF2=60°，则△F1PF2的面积为（ ）
| A． | $9\sqrt{3}$ | B． | 9 | C． | 18 | D． | 16 |
8．$y=sin（{2x+\frac{5π}{2}}）$的图象的一条对称轴是（ ）
| A． | $-\frac{π}{4}$ | B． | $-\frac{π}{2}$ | C． | $\frac{π}{8}$ | D． | $\frac{5π}{4}$ |