题目内容
已知a，b为正数，记L（a，b）=
为“正数a，b的对数平均数”．
（1）求函数f（x）=L（x，1），x∈（1，+∞）的单调区间；
（2）a≥b＞0，比较a，b的“算术平均数”，“几何平均数”和“对数平均数”的大小关系．
|
（1）求函数f（x）=L（x，1），x∈（1，+∞）的单调区间；
（2）a≥b＞0，比较a，b的“算术平均数”，“几何平均数”和“对数平均数”的大小关系．
考点：基本不等式
专题：导数的综合应用
分析：（1）根据已知条件求得f（x）=
，求f′（x）=
，所以要判断f′（x）的符号，只需判断lnx-
的符号．可令h（x）=lnx-
，h′（x）=
＞0，所以便得到h（x）在（1，+∞）上单调递增，所以h（x）＞h（1）=0，所以便得到f′（x）＞0，所以f（x）在（1，+∞）上是增函数，而增区间便是（1，+∞）；
（2）a=b时，容易得到
=
=L(a，b)，所以判断a＞b时的情况即可：根据基本不等式
＞
，所以需判断
和L（a，b），
和L（a，b）的大小关系，通过作差法进行比较.
-L(a，b)=
-
=
[ln
-
]，
＞0，所以只要判断ln
-
的符号即可．所以可令
=u，u＞1，G（u）=lnu-
，G′（u）=
＞0，所以G（u）＞G（1）=0，所以便可得到
＞L(a，b)，而同样的办法去比较
和L（a，b）的大小关系，最后便可得到这三个平均数的大小关系．
| x-1 |
| lnx |
lnx-
| ||
| (lnx)2 |
| x-1 |
| x |
| x-1 |
| x |
| x-1 |
| x2 |
（2）a=b时，容易得到
| a+b |
| 2 |
| ab |
| a+b |
| 2 |
| ab |
| a+b |
| 2 |
| ab |
| a+b |
| 2 |
| a+b |
| 2 |
| a-b |
| lna-lnb |
| a+b | ||
2ln
|
| a |
| b |
2(
| ||
|
| a+b | ||
2ln
|
| a |
| b |
2(
| ||
|
| a |
| b |
| 2(u-1) |
| u+1 |
| (u-1)2 |
| u(u+1)2 |
| a+b |
| 2 |
| ab |
解答：
解：（1）根据已知条件，∵x∈（1，+∞），∴L（x，1）=
；
∴f（x）=
，f′（x）=
；
设h（x）=lnx-
，h′（x）=
-
=
；
∵x＞1，∴h′（x）＞0，∴h（x）在（1，+∞）上是增函数，所以h（x）＞h（1）=0，即f′（x）＞0；
∴f（x）在（1，+∞）上是增函数，（1，+∞）是f（x）的单调递增区间；
（2）a=b＞0时，
=
=L(a，b)；
a＞b＞0时，
＞
；
-L(a，b)=
-
=
=
[ln
-
]=
[ln
-
]，设
=u，u＞1，则：
G（u）=lnu-
，G′（u）=
-
=
＞0；
∴函数G（u）在（1，+∞）上是增函数，∴G（u）＞G（1）=0，即ln
-
＞0；
又
＞1，
＞0，∴
＞L(a，b)；
-L(a，b)=
-
=
(ln
-
)=
(ln
-
)，设
=u，
=u2，（u＞1）则：
H（u）=lnu2-
=2lnu-u+
，H′（u）=
-1-
=
＜0；
∴函数H（u）在（1，+∞）上单调递减，∵H（u）＜H（1）=0，即ln
-
＜0；
又
＞0，∴
＜L(a，b)；
∴综上得a，b的“算术平均数”，“几何平均数”和“对数平均数”的大小关系为：
≥L(a，b)≥
，当a=b时取“=”．
| x-1 |
| lnx |
∴f（x）=
| x-1 |
| lnx |
lnx-
| ||
| (lnx)2 |
设h（x）=lnx-
| x-1 |
| x |
| 1 |
| x |
| 1 |
| x2 |
| x-1 |
| x2 |
∵x＞1，∴h′（x）＞0，∴h（x）在（1，+∞）上是增函数，所以h（x）＞h（1）=0，即f′（x）＞0；
∴f（x）在（1，+∞）上是增函数，（1，+∞）是f（x）的单调递增区间；
（2）a=b＞0时，
| a+b |
| 2 |
| ab |
a＞b＞0时，
| a+b |
| 2 |
| ab |
| a+b |
| 2 |
| a+b |
| 2 |
| a-b |
| lna-lnb |
(a+b)ln
| ||
2ln
|
| a+b | ||
2ln
|
| a |
| b |
| 2(a-b) |
| a+b |
| a+b | ||
2ln
|
| a |
| b |
2(
| ||
|
| a |
| b |
G（u）=lnu-
| 2(u-1) |
| u+1 |
| 1 |
| u |
| 4 |
| (u+1)2 |
| (u-1)2 |
| u(u+1)2 |
∴函数G（u）在（1，+∞）上是增函数，∴G（u）＞G（1）=0，即ln
| a |
| b |
2(
| ||
|
又
| a |
| b |
| a+b | ||
ln
|
| a+b |
| 2 |
| ab |
| ab |
| a-b |
| lna-lnb |
| ||
ln
|
| a |
| b |
| a-b | ||
|
| ||
ln
|
| a |
| b |
| ||||
|
|
| a |
| b |
H（u）=lnu2-
| u2-1 |
| u |
| 1 |
| u |
| 2 |
| u |
| 1 |
| u2 |
| -(u-1)2 |
| u2 |
∴函数H（u）在（1，+∞）上单调递减，∵H（u）＜H（1）=0，即ln
| a |
| b |
| ||||
|
又
| ||
ln
|
| ab |
∴综上得a，b的“算术平均数”，“几何平均数”和“对数平均数”的大小关系为：
| a+b |
| 2 |
| ab |
点评：考查通过判断导数符号来判断函数单调性的方法，以及对于g（x）=f′（x）的情况，根据函数g（x）的单调性来判断导数f′（x）符号的方法，以及通过构造函数来判断一个式子的符号的方法．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知集合A={0，1，2}，B{1，2，3}，则∁（A∪B）（A∩B）=（ ）
| A、{0，3} |
| B、{1，2} |
| C、∅ |
| D、{0，1，2，3} |
如图，△ADP为正三角形，O为正方形ABCD中心，而ADP⊥面ABCD，M为面ABCD内的点，且满足MP=MC．则点M在正方形ABCD内的轨迹为（ ）
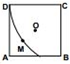
如图平行四边形ABCD中，∠DAB=60°，AB=2AD=2，M为边CD的中点，沿BM将△CBM折起使得平面BMC⊥平面ABMD．