题目内容
已知动点P到点A(-2,0)与点B(2,0)的斜率之积为-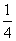 ,点P的轨迹为曲线C.
,点P的轨迹为曲线C.
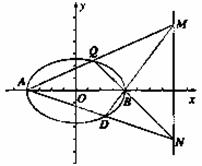
(1)求曲线C的方程;
(2)若点Q为曲线C上的一点,直线AQ,BQ与直线x=4分别交于M,N两点,直线BM与椭圆的交点为D.求证,A,D,N三点共线.
(1)解 设P点坐标(x,y),则kAP=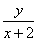 (x≠-2),kBP=
(x≠-2),kBP=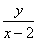 (x≠2),由已知
(x≠2),由已知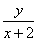 ·
·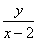 =-
=-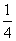 ,化简,得
,化简,得 +y2=1,所求曲线C的方程为
+y2=1,所求曲线C的方程为 +y2=1(x≠±2).
+y2=1(x≠±2).
 =
=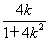 ,所以Q
,所以Q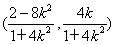 .
.
当x=4,得yM=6k,即M(4,6k).又直线BQ的斜率为-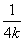 ,方程为y=-
,方程为y=-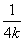 (x-2),当x=4时,得yN=-
(x-2),当x=4时,得yN=-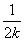 ,即N
,即N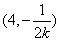 .直线BM的斜率为3k,方程为y=3k(x-2).
.直线BM的斜率为3k,方程为y=3k(x-2).

因为kAD=-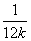 ,kAN=-
,kAN=-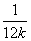 ,所以kAD=kAN. 所以A,D,N三点共线.
,所以kAD=kAN. 所以A,D,N三点共线.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 平面
平面 ,直线
,直线
 平面
平面 ,给出下列命题,其中正确的是 ( )
,给出下列命题,其中正确的是 ( ) ②
②
 ④
④
 同的概率;
同的概率; ,求
,求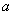 的正方体
的正方体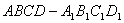 中,
中,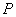 为
为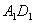 的中点,
的中点,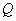 为
为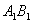 上任意一点,
上任意一点,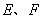 为
为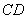 上任意两点,且
上任意两点,且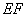 的长为定值,则下面四个值中不为定值的是
的长为定值,则下面四个值中不为定值的是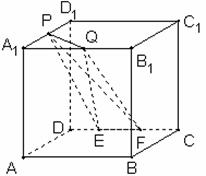
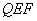 的距离
的距离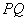 与平面
与平面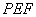 所成的角
所成的角 的体积
的体积 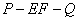 的大小
的大小 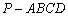 的底面
的底面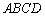 是边长为
是边长为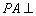 平面
平面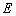 是
是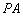 的中点.
的中点.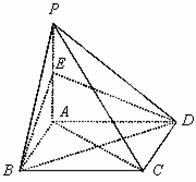
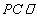 平面
平面 ;
;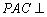 平面
平面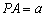 ,求三棱锥
,求三棱锥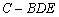 的体积.
的体积. .
.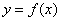 在
在 和
和 处的切线互相平行,求
处的切线互相平行,求 的值;
的值;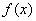 的单调区间;
的单调区间; ,若对任意
,若对任意 ,均存在
,均存在 ,使得
,使得 ,求
,求 的最大值为( )
的最大值为( ) B.
B. C.
C. D.
D.
 B.
B.  C.
C. D.1
D.1 中,角
中,角 的对边分别是
的对边分别是 ,且
,且 ,则
,则 等于( )
等于( ) B.
B. C.
C. D.
D.