题目内容
12.在等腰直角三角形ABC中,∠ACB=90°,在∠ACB内部任意作一条射线CM,与线段AB交于点M,则AM<AC的概率( )| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{4}$ |
分析 由于过直角顶点C在∠ACB内部任作一射线CM,故可以认为所有可能结果的区域为∠ACB,可将事件A构成的区域为∠ACC',以角度为“测度”来计
解答 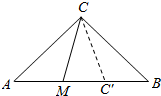 解:在AB上取AC'=AC,则∠ACC′=$\frac{180°-45°}{2}$=67.5°.
解:在AB上取AC'=AC,则∠ACC′=$\frac{180°-45°}{2}$=67.5°.
记A={在∠ACB内部任作一射线CM,与线段AB交于点M,AM<AC},
则所有可能结果的区域为∠ACB,
事件A构成的区域为∠ACC'.
又∠ACB=90°,∠ACC'=67.5°.
∴P(A)=$\frac{67.5°}{90°}$=$\frac{3}{4}$.
故选:C.
点评 本题考查了几何概型的概率求法;在利用几何概型的概率公式来求其概率时,几何“测度”可以是长度、面积、体积、角度等.

练习册系列答案
相关题目
3.从4个男生,3个女生中挑选4人参加智力竞赛,要求至少有一个女生参加的选法共有( )
| A. | 12种 | B. | 34种 | C. | 35种 | D. | 36种 |
7.已知函数f(x)=$\frac{1}{3}$x3+$\frac{1}{2}$ax2+$\frac{1}{4}$b2x(a,b∈R),若|a-1|+|b-1|≤1,求f′(x)在R上有零点的概率( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
4.设Sn是等差数列{an}的前n项和,若S2=2,S4=10,则S6等于( )
| A. | 4 | B. | 12 | C. | 18 | D. | 24 |
1.如果把两条平行的直线称为“一对”,那么在正方体的12条棱中,相互平行的直线共有( )对.
| A. | 6 | B. | 9 | C. | 12 | D. | 18 |