Question

8．设关于x，y的不等式组$\left\{\begin{array}{l}{2x-y+1＞0}\\{y-m＞0}\\{x+m＜0}\end{array}\right.$表示的平面区域内存在点P（x₀，y₀），满足x₀-2y₀=2，则m的取值范围是（　　）

• A． （-∞，$\frac{4}{3}$）
• B． （-∞，$\frac{1}{3}$）
• C． （-∞，-$\frac{2}{3}$）
• D． （-∞，-$\frac{5}{3}$）

Answer 1

分析 作出不等式组对应的平面区域，要使平面区域内存在点点P（x₀，y₀）满足x₀-2y₀=2，则平面区域内必存在一个点在直线x-2y=2的下方，由图象可得m的取值范围．

解答 解：作出不等式组对应的平面如图：交点C的坐标为（-m，m），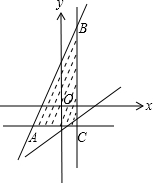

直线x-2y=2的斜率为$\frac{1}{2}$，斜截式方程为$y=\frac{1}{2}x-1$，
要使平面区域内存在点P（x₀，y₀）满足x₀-2y₀=2，
则点C（-m，m）必在直线x-2y=2的下方，
即m$＜-\frac{1}{2}m-1$，解得m$＜-\frac{2}{3}$．
故选：C．

点评 本题主要考查线性规划的基本应用，利用数形结合是解决本题的关键，综合性较强，属中高档题．