题目内容
19.若α是第二象限角,则-α,π+α,π-α,$\frac{π}{2}$+α分别是第几象限的角?分析 首先写出第二象限的角的集合,然后分别得到-α,π+α,π-α,$\frac{π}{2}$+α的范围得答案.
解答 解:∵α是第二象限角,
∴$\frac{π}{2}+2kπ<α<π+2kπ,k∈Z$,
则$-π-2kπ<-α<-\frac{π}{2}-2kπ,k∈Z$,-α是第三象限的角;
$\frac{3}{2}π+2kπ<π+α<2π+2kπ,k∈Z$,π+α是第四象限角;
$-2kπ<π-α<\frac{π}{2}-2kπ,k∈Z$,π-α是第一象限角;
$π+2kπ<\frac{π}{2}+α<\frac{3π}{2}+2kπ,k∈Z$,$\frac{π}{2}$+α是第三象限角.
点评 本题考查了象限角和轴线角,是基础的会考题型.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
12.已知抛物线x2=4y,过点P(0,2)作斜率分别为k1,k2的直线l1,l2,与抛物线分别交于两点,若k1k2 =-$\frac{3}{4}$,则四个交点构成的四边形面积的最小值为( )
| A. | 18$\sqrt{3}$ | B. | 20$\sqrt{3}$ | C. | 22$\sqrt{3}$ | D. | 24$\sqrt{3}$ |
11.已知M(2,4)是抛物线y2=8x上一定点,A,B是抛物线上异于M的两个动点,若MA⊥MB,直线AB必过的定点的坐标为( )
| A. | (8,-4) | B. | (10,-4) | C. | (10,4) | D. | (8,4) |
 (
( 为自然对数的底数).
为自然对数的底数). 时,求过点
时,求过点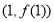 处的切线与坐标轴围成的三角形的面积;
处的切线与坐标轴围成的三角形的面积; 在
在 上恒成立,求实数
上恒成立,求实数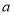 的取值范围.
的取值范围. 如图,过抛物线y2=2px(p>0)的焦点F的直线与抛物线相交于M、N两点,自M、N向准线L作垂线,垂足分别为M1、N1,求证:FM⊥FN.
如图,过抛物线y2=2px(p>0)的焦点F的直线与抛物线相交于M、N两点,自M、N向准线L作垂线,垂足分别为M1、N1,求证:FM⊥FN.