题目内容
4.给出定义:若m-$\frac{1}{2}<$x≤m+$\frac{1}{2}$(其中m为整数),则m叫做离实数x最近的整数,记作{x},即{x}=m.在此基础上给出下列关于函数f(x)=|x-{x}|的四个命题.①函数y=f(x)的定义域是R,值域是[0,$\frac{1}{2}$]
②函数y=f(x)的图象关于x=$\frac{k}{2}$(k∈Z)对称;
③函数y=f(x)的图象关于点($\frac{k}{2}$,0)(k∈Z)对称;
④函数y=f(x)是周期函数,最小正周期是1;
⑤函数y=f(x)在[-$\frac{1}{2}$,$\frac{1}{2}$]上是增函数;
其中真命题是(填上所有真命题的序号)①②④.
分析 根据题意,先对函数化简,然后作出函数的图象,根据函数的图象可判断各个选项是否正确
解答 解:∵函数f(x)=|x-{x}|的图象如下图所示: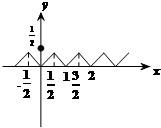
由图可知:
①函数y=f(x)的定义域是R,值域是[0,$\frac{1}{2}$],故正确;
②函数y=f(x)的图象关于x=$\frac{k}{2}$(k∈Z)对称,故正确;
③函数y=f(x)的图象关于点($\frac{k}{2}$+$\frac{1}{4}$,0)(k∈Z)对称,故错误;
④函数y=f(x)是周期函数,最小正周期是1,故正确;
⑤函数y=f(x)在[-$\frac{1}{2}$,0]上是减函数,在[0,$\frac{1}{2}$]上是增函数,故错误;
故答案为:①②④
点评 本题考查函数的性质和应用,解题时要认真审题,仔细解答,注意函数的定义域、值域、对称性和周期性的求法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,若
,若 是从
是从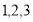 三个数中任取的一个数,
三个数中任取的一个数, 是从
是从 三个数中任取的一个数,则使函数
三个数中任取的一个数,则使函数 有极值点的概率为_______.
有极值点的概率为_______.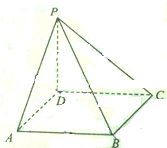 如图,四棱锥P-ABCD中底面是变长为a的正方形,且PD=a,PA=PC=$\sqrt{2}a$,求平面APB与平面PBD夹角的大小.
如图,四棱锥P-ABCD中底面是变长为a的正方形,且PD=a,PA=PC=$\sqrt{2}a$,求平面APB与平面PBD夹角的大小. 如图,在圆内接四边形ABCD中,AB∥DC,过点A作圆的切线与CB的延长线交于点E.若AB=AD=BC=5,AE=6,则BE=4DC=$\frac{25}{4}$.
如图,在圆内接四边形ABCD中,AB∥DC,过点A作圆的切线与CB的延长线交于点E.若AB=AD=BC=5,AE=6,则BE=4DC=$\frac{25}{4}$. 的连续可导函数
的连续可导函数 ,若满足以下两个条件:
,若满足以下两个条件: 没有零点,②对
没有零点,②对 ,都有
,都有 .
. 方程
方程 有( )个解.
有( )个解.