题目内容
8. 如图,过抛物线y2=2px(p>0)的焦点F的直线与抛物线相交于M、N两点,自M、N向准线L作垂线,垂足分别为M1、N1,求证:FM⊥FN.
如图,过抛物线y2=2px(p>0)的焦点F的直线与抛物线相交于M、N两点,自M、N向准线L作垂线,垂足分别为M1、N1,求证:FM⊥FN.
分析 由抛物线的定义可得:|MF|=|MM1|,|NF|=|NN1|,可得∠MFM1=∠MM1F,∠NFN1=∠NN1F.利用MM1∥NN1,可得$∠FM{M}_{1}+∠FN{N}_{1}=18{0}^{°}$,即可证明.
解答 证明:由抛物线的定义可得:|MF|=|MM1|,|NF|=|NN1|,
∴∠MFM1=∠MM1F,∠NFN1=∠NN1F,
∵MM1∥NN1,
∴$∠FM{M}_{1}+∠FN{N}_{1}=18{0}^{°}$,
∴∠MFM1+∠NFN1=$\frac{1}{2}(18{0}^{°}-∠FM{M}_{1})$+$\frac{1}{2}(18{0}^{°}-∠FN{N}_{1})$=180°-90°=90°,
∴FM⊥FN.
点评 本题考查了抛物线的定义、平行线的性质、三角形的内角和定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目




 是抛物线
是抛物线 的焦点,
的焦点, 是
是 上的两个点,线段
上的两个点,线段 的中点为
的中点为 ,则
,则 的面积等于 .
的面积等于 .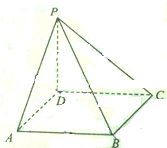 如图,四棱锥P-ABCD中底面是变长为a的正方形,且PD=a,PA=PC=$\sqrt{2}a$,求平面APB与平面PBD夹角的大小.
如图,四棱锥P-ABCD中底面是变长为a的正方形,且PD=a,PA=PC=$\sqrt{2}a$,求平面APB与平面PBD夹角的大小.