题目内容

数列{an}满足:a1=2,a1+a2+a3=12且an-2an+1+an+2=0(n∈N*).

(1)求数列{an}的通项公式；

（2）令bn=，求{bn}的前 n项和Sn.

解析:(1)由2an+1=an+an+2知，数列{an}是等差数列，又a1+a2+a3=12,且a1=2,

∴3a1+3d=12.

∴3d=6.

∴d=2.

∴an=a1+(n-1)d=2+(n-1)·2=2n.

(2)bn=,

∴Sn=b1+b2+…+bn=(1-)+(-)+…+(-)=1-.

练习册系列答案
相关题目
数列{an}满足a 1=
3
2
，a n+1=
a
2
n
-an+1（n∈N*），则m=
1
a1
+
1
a2
+
1
a3
+…+
1
a2012
的整数部分是（　　）
已知正项数列{an}满足
a
 
1
=P(0＜P＜1)，且
a
 
n+1
=
a
 
n
a
 
n
+1
，
（1）求数列的通项an；
（2）求证：
a
 
1
2
+
a
 
2
3
+
a
 
3
4
+…+
a
 
n
n+1
＜1．
（2012•三明模拟）若数列{an}满足a≤an≤b，其中a、b是常数，则称数列{an}为有界数列，a是数列{an}的下界，b是数列{an}的上界．现要在区间[-1，2）中取出20个数构成有界数列{bn}，并使数列{bn}有且仅有两项差的绝对值小于
1
m
，那么正数m的最小取值是（　　）
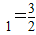数列{an}满足a，a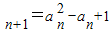（n∈N*），则m=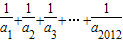的整数部分是（ ）
A．3
B．2
C．1
D．0
若数列{an}满足a≤an≤b，其中a、b是常数，则称数列{an}为有界数列，a是数列{an}的下界，b是数列{an}的上界．现要在区间[-1，2）中取出20个数构成有界数列{bn}，并使数列{bn}有且仅有两项差的绝对值小于，那么正数m的最小取值是（ ）
A．5
B．
C．7
D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网