题目内容
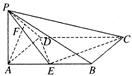
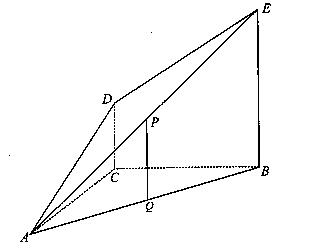
(本小题满分12分)如图4,四棱锥P—ABCD中,底面ABCD是直角梯形,AB//CD,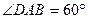 ,AB=AD=2CD,侧面
,AB=AD=2CD,侧面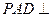 底面ABCD,且
底面ABCD,且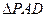 为等腰直角三角形,
为等腰直角三角形,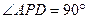 ,M为AP的中点。
,M为AP的中点。
 (1)求证:
(1)求证: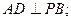
(2)求证:DM//平面PCB;
(3)求平面PAD与平面PBC所成锐二面角的大小。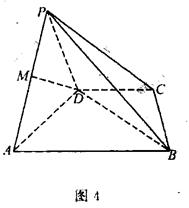
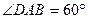 ,AB=AD=2CD,侧面
,AB=AD=2CD,侧面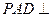 底面ABCD,且
底面ABCD,且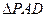 为等腰直角三角形,
为等腰直角三角形,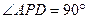 ,M为AP的中点。
,M为AP的中点。 (1)求证:
(1)求证: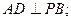
(2)求证:DM//平面PCB;
(3)求平面PAD与平面PBC所成锐二面角的大小。

同解析
解法一:(1)取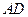 的中点
的中点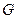 ,连结
,连结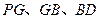 .
.
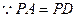 ,
, 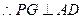 …………2分
…………2分
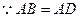 ,且
,且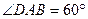 ,
,
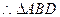 是正三角形,
是正三角形,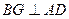 ,又
,又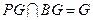 ,
,
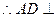 平面
平面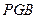 .
.
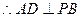 . …………4分
. …………4分
(2)取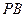 的中点
的中点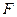 ,连结
,连结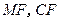 .
.
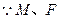 分别为
分别为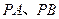 的中点,
的中点,
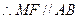 ,且
,且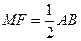 .
.
∵四边形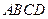 是直角梯形,
是直角梯形,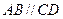 且
且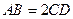 ,
,
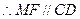 且
且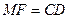 . …………6分
. …………6分
∴四边形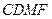 是平行四边形.
是平行四边形.
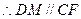 .
.
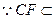 平面
平面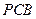 ,
,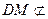 平面
平面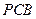
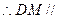 平面
平面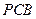 . …………8分
. …………8分
(3)延长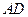 与
与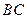 交点为
交点为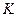 ,连结
,连结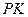 .
.
过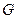 作
作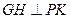 于一定
于一定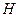 ,
,
连结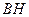 ,则
,则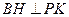 .
.
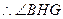 为平面
为平面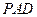 与平面
与平面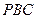 所成锐二面角的平面角. …………0分
所成锐二面角的平面角. …………0分
设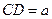 ,则
,则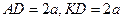 ,
,
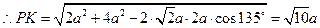 .
.
又因为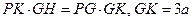 ,
,
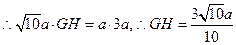
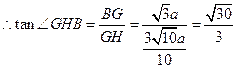
 平面
平面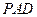 与平面
与平面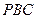 所成锐二面角的大小为
所成锐二面角的大小为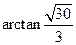 . …………12分
. …………12分
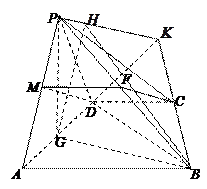
解法二:(1)同解法一
(2) ∵侧面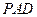
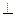 底面
底面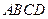 ,
,
又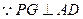 ,
, 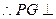 底面
底面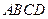 .
.
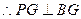 .
.
∴直线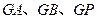 两两互相垂直,
两两互相垂直,
故以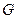 为原点,直线
为原点,直线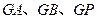 所在直线为
所在直线为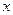 轴、
轴、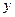 轴和
轴和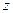 轴建立如图所示的空间直角坐标系
轴建立如图所示的空间直角坐标系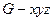 .
.
设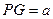 ,则可求得
,则可求得
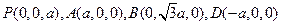 ,
,
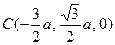 .
.
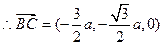 .
.
设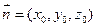 是平面
是平面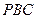 的法向量,则
的法向量,则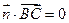 且
且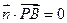 .
.
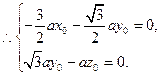
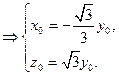
取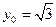 ,得
,得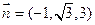 . …………6分
. …………6分
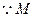 是
是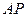 的中点,
的中点,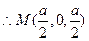 .
.
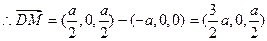 .
.
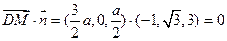 .
.
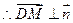 .
.
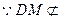 平面
平面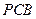 ,
,
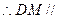 平面
平面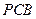 . ………………………8分
. ………………………8分
(3)又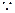 平面
平面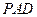 的法向量
的法向量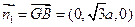 ,
,
设平面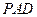 与平面
与平面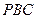 所成锐二面角为
所成锐二面角为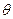 ,
,
则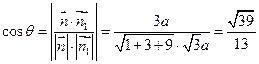 ,…………10分
,…………10分
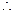 平面
平面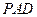 与平面
与平面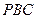 所成锐二面角的大小为
所成锐二面角的大小为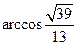 .…………12分
.…………12分

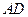 的中点
的中点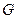 ,连结
,连结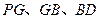 .
.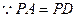 ,
, 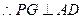 …………2分
…………2分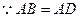 ,且
,且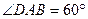 ,
,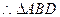 是正三角形,
是正三角形,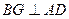 ,又
,又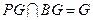 ,
,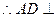 平面
平面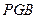 .
.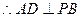 . …………4分
. …………4分(2)取
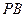 的中点
的中点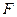 ,连结
,连结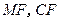 .
.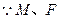 分别为
分别为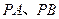 的中点,
的中点,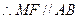 ,且
,且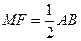 .
.∵四边形
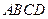 是直角梯形,
是直角梯形,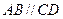 且
且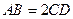 ,
,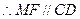 且
且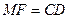 . …………6分
. …………6分∴四边形
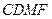 是平行四边形.
是平行四边形.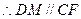 .
.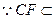 平面
平面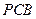 ,
,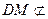 平面
平面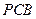
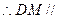 平面
平面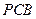 . …………8分
. …………8分(3)延长
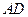 与
与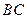 交点为
交点为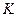 ,连结
,连结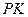 .
.过
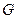 作
作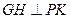 于一定
于一定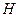 ,
,连结
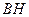 ,则
,则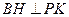 .
.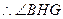 为平面
为平面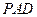 与平面
与平面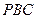 所成锐二面角的平面角. …………0分
所成锐二面角的平面角. …………0分设
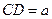 ,则
,则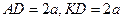 ,
,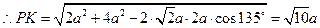 .
.又因为
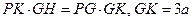 ,
,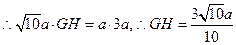
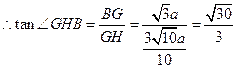
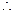 平面
平面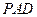 与平面
与平面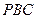 所成锐二面角的大小为
所成锐二面角的大小为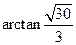 . …………12分
. …………12分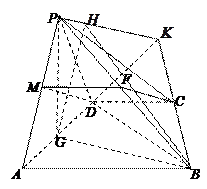
解法二:(1)同解法一
(2) ∵侧面
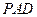
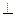 底面
底面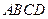 ,
,又
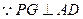 ,
, 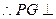 底面
底面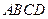 .
.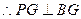 .
.∴直线
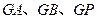 两两互相垂直,
两两互相垂直,故以
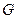 为原点,直线
为原点,直线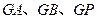 所在直线为
所在直线为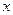 轴、
轴、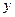 轴和
轴和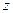 轴建立如图所示的空间直角坐标系
轴建立如图所示的空间直角坐标系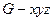 .
.设
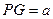 ,则可求得
,则可求得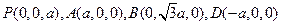 ,
,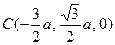 .
.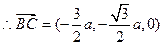 .
.设
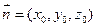 是平面
是平面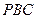 的法向量,则
的法向量,则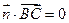 且
且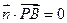 .
.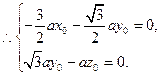
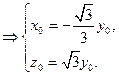
取
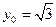 ,得
,得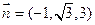 . …………6分
. …………6分 是
是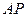 的中点,
的中点,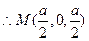 .
.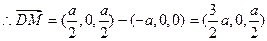 .
.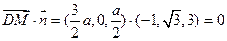 .
.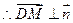 .
.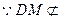 平面
平面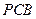 ,
,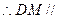 平面
平面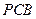 . ………………………8分
. ………………………8分(3)又
 平面
平面 的法向量
的法向量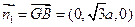 ,
,设平面
 与平面
与平面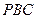 所成锐二面角为
所成锐二面角为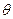 ,
,则
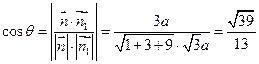 ,…………10分
,…………10分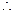 平面
平面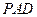 与平面
与平面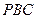 所成锐二面角的大小为
所成锐二面角的大小为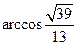 .…………12分
.…………12分

练习册系列答案
相关题目
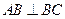 ,
,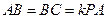 ,点
,点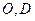 分别是AC、PC的中点,
分别是AC、PC的中点,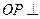 底面AB
底面AB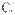
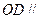 平面
平面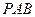 ;
;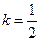 时,求
时,求 直线
直线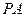 与平面
与平面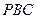 所成的角的大小;
所成的角的大小;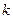 取何值时,
取何值时,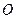 在平面
在平面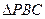 的重心?
的重心?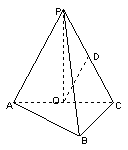
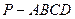 中,底面
中,底面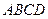 为矩形,
为矩形,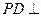 底面
底面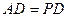 ,
,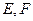 分别为
分别为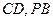 的中点
的中点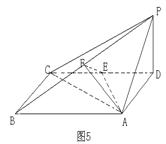
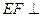 面
面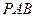 ;
; ,求
,求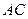 与面
与面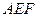 所成角的余弦值
所成角的余弦值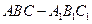 是正三棱柱(底面为正三角形,侧棱垂直于底面),它的底面边长和侧棱长都是
是正三棱柱(底面为正三角形,侧棱垂直于底面),它的底面边长和侧棱长都是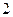 .
.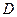 为侧棱
为侧棱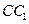 的中点,
的中点,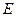 为底面一边
为底面一边 的中点.
的中点.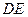 与
与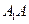 所成的角;
所成的角;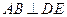 ;
; 的距离.
的距离.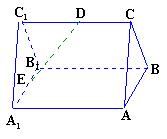
 中,
中,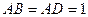 ,
,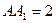 ,点
,点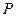 为
为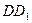 的中点。
的中点。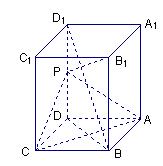
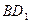 ∥平面
∥平面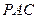 ;
;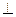 平面
平面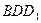 ;
;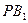
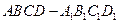 内接于球
内接于球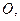
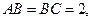
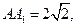 则
则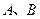 两点之间的球面距离
两点之间的球面距离 体的三视图(单位:cm)如图所示,则此
体的三视图(单位:cm)如图所示,则此