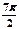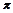题目内容
(本小题满分12分)
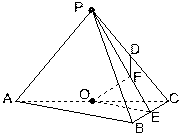
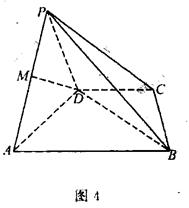
如图,在三棱锥P-ABC中,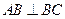 ,
,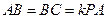 ,点
,点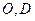 分别是AC、PC的中点,
分别是AC、PC的中点,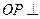 底面AB
底面AB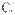
(1)求证: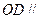 平面
平面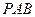 ;
;
(2)当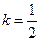 时,求
时,求 直线
直线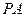 与平面
与平面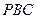 所成的角的大小;
所成的角的大小;
(3)当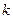 取何值时,
取何值时,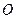 在平面
在平面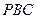 内的射影恰好为
内的射影恰好为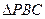 的重心?
的重心?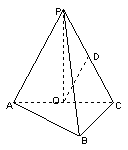
如图,在三棱锥P-ABC中,
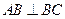 ,
,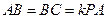 ,点
,点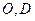 分别是AC、PC的中点,
分别是AC、PC的中点,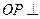 底面AB
底面AB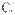
(1)求证:
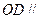 平面
平面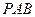 ;
;(2)当
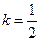 时,求
时,求 直线
直线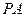 与平面
与平面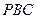 所成的角的大小;
所成的角的大小;(3)当
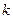 取何值时,
取何值时,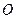 在平面
在平面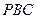 内的射影恰好为
内的射影恰好为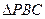 的重心?
的重心?
(1)证明见解析。
(2)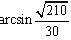
(3)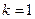
(2)
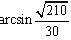
(3)
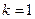
19.解 :方法一:
:方法一:
(Ⅰ) ∵O、D分别为AC、PC中点,
∵O、D分别为AC、PC中点,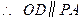
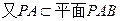 ,
,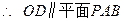 ………………………………(2分)
………………………………(2分)
(Ⅱ)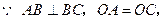
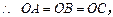
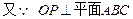
 ,
,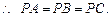
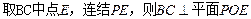
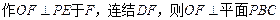
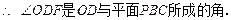 ………..(5分)
………..(5分)
又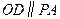 ,
,
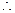 PA与平面PBC所成的角的大小等于
PA与平面PBC所成的角的大小等于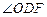 ,
,
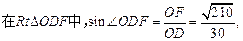
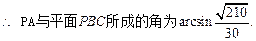 ………………(8分)
………………(8分)
(Ⅲ)由(Ⅱ)知,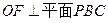 ,∴F是O在平面PBC内的射影
,∴F是O在平面PBC内的射影
∵D是PC的中点,
若点F是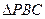 的重心,则B,F,D三点共线,
的重心,则B,F,D三点共线,
∴直线OB在平面PBC内的射影为直线BD,
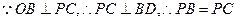 ,即
,即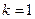 ………………….
…………………. .(10分)
.(10分)
反之,当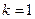 时,三棱锥
时,三棱锥 为正三棱锥,
为正三棱锥,
∴O在平面PBC内的射影为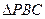 的重心…………………………..(12分)
的重心…………………………..(12分)
方法二:
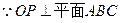 ,
,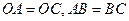 ,
,
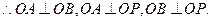
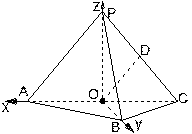
以O为原点,射线OP为非负z轴,建立空间直角坐标系 (如图)
(如图)
设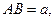 则
则 ,
,
设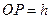 ,则
,则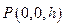
(Ⅰ)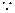 D为PC的中点,
D为PC的中点,
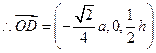 ,
,
又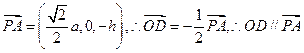 ,
,
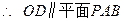
(Ⅱ)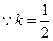 ,即
,即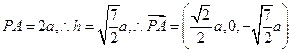 ,
,
可求得平面PBC的法向量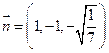 ,
,
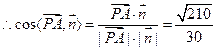 ,
,
设PA与平面PBC所成的角为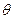 ,则
,则
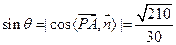 ,
,
(Ⅲ)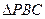 的重心
的重心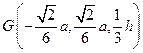 ,
,
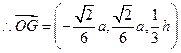 ,
,
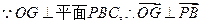 ,
,
又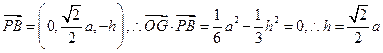 ,
,
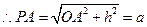 ,即
,即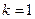 ,
,
反之,当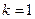 时,三棱锥
时,三棱锥 为正三棱锥,
为正三棱锥,
∴O在平面PBC内的射影为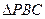 的重心
的重心
 :方法一:
:方法一:(Ⅰ)
 ∵O、D分别为AC、PC中点,
∵O、D分别为AC、PC中点,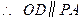
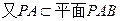 ,
,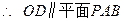 ………………………………(2分)
………………………………(2分)(Ⅱ)
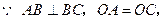
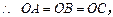
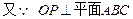
 ,
,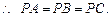
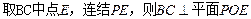
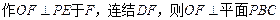

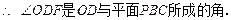 ………..(5分)
………..(5分)又
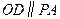 ,
,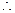 PA与平面PBC所成的角的大小等于
PA与平面PBC所成的角的大小等于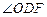 ,
,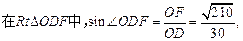
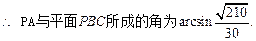 ………………(8分)
………………(8分)(Ⅲ)由(Ⅱ)知,
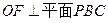 ,∴F是O在平面PBC内的射影
,∴F是O在平面PBC内的射影∵D是PC的中点,
若点F是
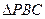 的重心,则B,F,D三点共线,
的重心,则B,F,D三点共线,∴直线OB在平面PBC内的射影为直线BD,
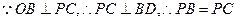 ,即
,即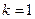 ………………….
…………………. .(10分)
.(10分)反之,当
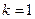 时,三棱锥
时,三棱锥 为正三棱锥,
为正三棱锥,∴O在平面PBC内的射影为
 的重心…………………………..(12分)
的重心…………………………..(12分)方法二:
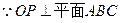 ,
,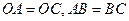 ,
,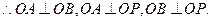
以O为原点,射线OP为非负z轴,建立空间直角坐标系
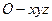 (如图)
(如图)
设
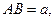 则
则 ,
,设
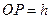 ,则
,则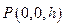
(Ⅰ)
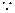 D为PC的中点,
D为PC的中点,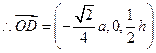 ,
,又
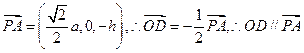 ,
,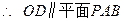
(Ⅱ)
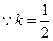 ,即
,即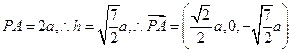 ,
,可求得平面PBC的法向量
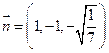 ,
,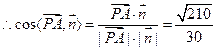 ,
,设PA与平面PBC所成的角为
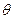 ,则
,则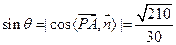 ,
,(Ⅲ)
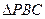 的重心
的重心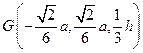 ,
,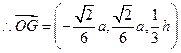 ,
,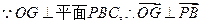 ,
,又
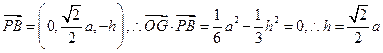 ,
,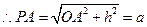 ,即
,即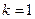 ,
,反之,当
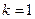 时,三棱锥
时,三棱锥 为正三棱锥,
为正三棱锥,∴O在平面PBC内的射影为
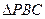 的重心
的重心
练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
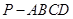 中,底面
中,底面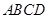 是
是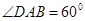 且边长为
且边长为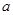 的菱形,侧面
的菱形,侧面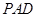 是等边三角形,且平面
是等边三角形,且平面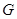 为
为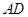 的中点,求证:
的中点,求证: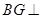 平面
平面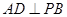 ;
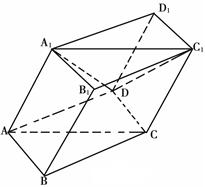
;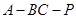 的大小.
的大小.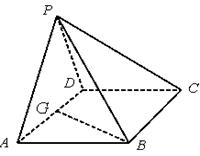
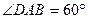 ,AB=AD=2CD,侧面
,AB=AD=2CD,侧面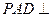 底面ABCD,且
底面ABCD,且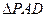 为等腰直角三角形,
为等腰直角三角形,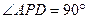 ,M为AP的中点。
,M为AP的中点。 (1)求证:
(1)求证: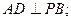
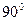 ,二面角P—BC—A为
,二面角P—BC—A为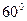 ,△PBC和△ABC的面积分别为16和10,BC=4. 求:
,△PBC和△ABC的面积分别为16和10,BC=4. 求: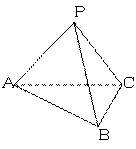 (1)PA的长;(2)三棱锥P—ABC的体积
(1)PA的长;(2)三棱锥P—ABC的体积
 底面ABCD,点M是棱PC的中点,AM
底面ABCD,点M是棱PC的中点,AM
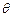 的余弦值.
的余弦值.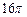 的球面上有三点A、B、C,∠ACB=60°,AB=
的球面上有三点A、B、C,∠ACB=60°,AB=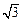 ,则球心到截面ABC的距离及B、C两点间球面距离最大值分别为 ( )
,则球心到截面ABC的距离及B、C两点间球面距离最大值分别为 ( )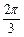
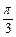

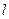 ⊥平面
⊥平面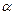 内所有直线”的充要条件是“
内所有直线”的充要条件是“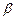 ”的必要不充分条件是“
”的必要不充分条件是“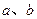 是异面直线,
是异面直线,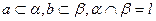 则
则 个顶点三条棱长分别为1,2,3,该长方体的顶点都在同一个球面上,则这个球的表面积为(s=4
个顶点三条棱长分别为1,2,3,该长方体的顶点都在同一个球面上,则这个球的表面积为(s=4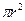 ) ( )
) ( )