题目内容
3．在等差数列{an}中，${a_9}=\frac{1}{2}{a_{12}}+6$，则数列{an}的前11项和S11=（ ）| A． | 132 | B． | 66 | C． | 48 | D． | 24 |
分析 利用等差数列的通项公式求出a1+5d=12，由此能求出数列{an}的前11项和S11．
解答 解：等差数列{an}中，${a_9}=\frac{1}{2}{a_{12}}+6$，
∴${a}_{1}+8d=\frac{1}{2}（{a}_{1}+11d）+6$，
解得a1+5d=12，
∴数列{an}的前11项和S11=$\frac{11}{2}（{a}_{1}+{a}_{11}）$=$\frac{11}{2}（2{a}_{1}+10d）$=132．
故选：A．
点评 本题考查数列的前11项和的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．
练习册系列答案
相关题目
13．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|=2|$\overrightarrow{b}$|≠0，且关于x的函数f（x）=2x3-3|$\overrightarrow{a}$|x2+6$\overrightarrow{a}$•$\overrightarrow{b}$x+5在实数集R上有极值，则向量$\overrightarrow{a}$，$\overrightarrow{b}$的夹角的取值范围是（ ）
| A． | （$\frac{π}{3}$，π） | B． | （$\frac{π}{3}$，π] | C． | [$\frac{π}{3}$，π] | D． | （0，$\frac{π}{3}$） |
8．在平面直角坐标系xOy中，已知点A（0，-1），B点在直线y=1上，M点满足$\overrightarrow{MB}$∥$\overrightarrow{OA}$，$\overrightarrow{MA}$•$\overrightarrow{AB}$=$\overrightarrow{MB}$•$\overrightarrow{BA}$，M点的轨迹方程为（ ）
| A． | y2=4x | B． | x2=-4y | C． | x2+4y2=1 | D． | x2-4y2=1 |
12．甲、乙两名运动员在某项测试中的6次成绩的茎叶图如图所示，${\overline{x}}_{1}$，${\overline{x}}_{2}$分别表示甲、乙两名运动员这项测试成绩的平均数，s${\;}_{1}^{2}$，s${\;}_{2}^{2}$分别表示甲、乙两名运动员这项测试成绩的方差，则有（ ）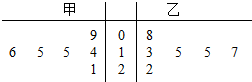
| A． | ${\overline{x}}_{1}$＞${\overline{x}}_{2}$，s${\;}_{1}^{2}$＜${s}_{2}^{2}$ | B． | ${\overline{x}}_{1}$=${\overline{x}}_{2}$，s${\;}_{1}^{2}$＞${s}_{2}^{2}$ | ||
| C． | ${\overline{x}}_{1}$=${\overline{x}}_{2}$，s${\;}_{1}^{2}$=${s}_{2}^{2}$ | D． | ${\overline{x}}_{1}$=${\overline{x}}_{2}$，s${\;}_{1}^{2}$＜${s}_{2}^{2}$ |
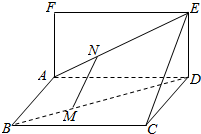如图，已知矩形ABCD和矩形ADEF所在平面互相垂直，点M，N分别在对角线BD、AE上，且BM=$\frac{1}{3}$BD，AN=$\frac{1}{3}$AE，求证：MN∥平面CDE．