题目内容
5．函数f（x）=（$\frac{1}{2}$）x在区间[-2，-1]上的最小值为2．分析 根据指数函数的单调性即可求出最值．
解答 解：$f（x）={（\frac{1}{2}）^x}$在区间[-2，-1]为减函数，
∴f（x）min=f（-1）=2，
故答案为：2．
点评 本题考查了指数函数的单调性以及最值求法，属于基础题．
练习册系列答案
名师伴你成长课时同步学练测系列答案
相关题目
15．
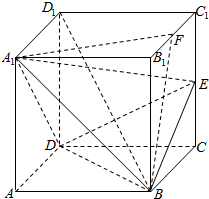已知正方体ABCD-A1B1C1D1的棱长为2a，E为CC1的中点，F为B1C1的中点．
（1）求证；BD⊥A1E；
（2）求证：平面A1BD⊥平面EBD；
（3）求证：平面A1BF⊥平面A1BD．
已知正方体ABCD-A1B1C1D1的棱长为2a，E为CC1的中点，F为B1C1的中点．（1）求证；BD⊥A1E；
（2）求证：平面A1BD⊥平面EBD；
（3）求证：平面A1BF⊥平面A1BD．
13．$\int_0^1{3{x^2}dx-\int_0^1{\sqrt{1-{x^2}}dx=}}$（ ）
| A． | $1-\frac{π}{4}$ | B． | 2 | C． | $1+\frac{π}{4}$ | D． | π-1 |
20．若全集U={0，1，2，3，4，5}，M={0，1}，则∁UM=（ ）
| A． | {0，1} | B． | {2，3，4，5} | C． | {0，2，3，4，5} | D． | {1，2，3，4，5} |
已知函数$f（x）=\left\{\begin{array}{l}x-1，x≥1\\-x+1，x＜1\end{array}\right.$．
17．函数y=lnx+2x-6零点的个数为（ ）
| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
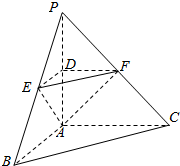如图，在三棱锥P-ABC中，平面PAC⊥平面ABC，PA⊥BC，AB⊥AC，PA=1，BC=2．D、E、F分别是棱PA、PB、PC的中点，连接DE、DF、EF．