Question

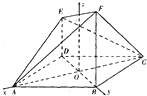
如图所示的多面体中，ABCD是菱形，ED∥FB，ED⊥面ABCD，AD=BD=2，BF=2DE=2

2

．
（Ⅰ）求证：AE⊥CF；
（Ⅱ）求二面角A-FC-E的余弦值．

Answer 1

考点：与二面角有关的立体几何综合题

专题：空间角

分析：（Ⅰ）以O为坐标原点，以OA，OB所在直线为x轴，y轴，建立空间直角坐标系，由此能证明AE⊥FC．
（Ⅱ）求出平面AFC的一个法向量和平面EFC的一个法向量，由此能求出二面角A-FC-E的余弦值．

解答： （Ⅰ）证明：∵ABCD是菱形，AD=BD=2，∴AC⊥BD，AC=2

3

，
∵ED⊥平面ABCD，BD=2，BF=2DE=2

2

，
∴以O为坐标原点，以OA，OB所在直线为x轴，y轴，建立如图所示的空间直角坐标系，
则A（

3

，0，0），E（0，-1，

2

），C（-

3

，0，0），F（0，1，2

2

），
∴

AE

=(-

3

，-1，

2

)，

CF

=(

3

，1，2

2

)，
∴

AE

•

CF

=-3-1+4=0，
∴AE⊥CF．
（Ⅱ）解：由（Ⅰ）知A（

3

，0，0），C（-

3

，0，0），F（0，2，

2

），

EC

=(-

3

，1，-

2

)，
设平面AFC的一个法向量为

n1

=（x₁，y₁，z₁），
由

AF

•

n1

=0，

AC

•

n1

=0，得

- 3 x   1 +y1+2 2 z1=0 -2 3 x1=0

，
令z₁=1，得

n1

=（0，-2

2

，1），
设平面EFC的一个法向量为

n2

=（x₂，y₂，z₂），
由

EF

•

n1

=0，

EC

•

n2

=0，
得

2y2+ 2 z2=0 - 3 x2+y2- 2 z2=0

，
令y₂=-1，得

n2

=（-

3

，-1，

2

），
设二面角A-FC-E的大小为θ，则：
cosθ=cos＜

n1

，

n2

＞=

0+2 2 + 2

3• 6

=

3

3

．

点评：本题考查异面直线垂直的证明，考查二面角的余弦值的求法，解题时要认真审题，注意向量法的合理运用．