题目内容
已知数列{ an}的前n项和Sn满足log2(Sn+1)=n+1,求{an}的通
an}的前n项和Sn满足log2(Sn+1)=n+1,求{an}的通 项公式.
项公式.
解析:由题意,得 Sn=2n+1-1,
Sn=2n+1-1,
当n≥2时,an=Sn-Sn-1=(2n+1-1)-(2n-1) =2n,
=2n,
当n=1时,a1=S1=3,不适合上式.
∴an=

练习册系列答案
相关题目
等差 数列{an}中,a1,a2,a3分别是下表第一、二、三行中的某一个数,且a1,a2,a3中的任何两个数不在下表的同一列.
数列{an}中,a1,a2,a3分别是下表第一、二、三行中的某一个数,且a1,a2,a3中的任何两个数不在下表的同一列.
|
| 第一列 | 第二列 | 第三列 |
| 第一行 |
| 3 | 5 |
| 第二行 | 8 | 6 | 14 |
| 第三行 | 11 | 9 | 13 |
则a4的值为( )
A.18 B.15 C.12 D.20
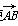 ·
· =-1,则|
=-1,则| |的
|的 最小值为__________.
最小值为__________.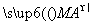 =2
=2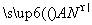 ,求点N的轨迹方程.
,求点N的轨迹方程. n,则当an取得最大值时,n等于( )
n,则当an取得最大值时,n等于( ) =____________.
=____________.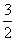 an-1(n∈N*).
an-1(n∈N*). 在点(3,2)处的切线与直线ax+y+1=0垂直,则a等于( )
在点(3,2)处的切线与直线ax+y+1=0垂直,则a等于( )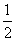 D.
D.