题目内容
已知数列{an}的前n项和为Sn，且Sn＝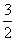
an－1(n∈N*)．
(1)求数列{an}的通项公式；
(2)在数列{bn}中，b1＝5，bn＋1＝bn＋an，求数列{bn}的通项公式．
解析：(1)当n＝1时，a1＝S1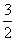＝a1－1，得a1＝2
.
当n≥2时，由Sn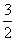＝an－1，①
得Sn－1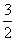＝an－1－1，②
①－②，并整理
得an＝3an－1，又a1≠0，故an－1≠0，
所以
＝3，
故数列{an}是首项为2，公比为3的等比数列，
所以an＝2·3n－1(n∈N*)．
(2)由(1)知bn＋1＝bn＋2·3n－1，
当n≥2时，bn＝bn－1＋2·3n－2，
…
b3＝b2＋2·31，
b2＝b1＋2·30，
以上各式相加并整理，得
bn＝b1＋2·(3n－2＋3n－3＋…＋31＋30)＝5＋2×
＝3n－1＋4，
当n＝1时，31－1＋4＝5＝b1，
所以bn＝3n－1＋4(n∈N*)．
练习册系列答案
相关题目
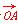＝(3,4)，
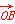＝(6，－3)，
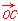＝(5－m，－3－m)．若点A，B，C能构成三角形，求实数m满足的条件．
an}的前n项和Sn满足log2(Sn＋1)＝n＋1，求{an}的通
项公式．
，则q＝__________.
，且S1，S2，S4成等比数列，求{an}的通项公式．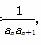
，且数列{bn}的前n项和为Tn，若Tn＝
－
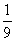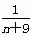，求数列{an}的公差．