Question

已知cos（α+β）=，cos（α-β）=，求tanαtanβ的值.

Answer 1

思路分析：要求tanαtanβ，需求sinαsinβ与cosαcosβ，两个整体式子的值，而cos（α+β）与cos（α-β）展开式中正好含有cosαcosβ与sinαsinβ，因此，可构造关于sinαsinβ，cosαcosβ的方程组来求解.

解：由条件得：

①+②得，2cosαcosβ=，∴cosαcosβ=.

②-①得，2sinαsinβ=，∴sinαsinβ=.

∴tanαtanβ=.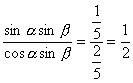

温馨提示

   要抓住公式之间的内在联系，在充分理解的基础上加强记忆，并能做到灵活运用公式本题就是利用方程的思想，构造一个关于sinαsinβ与cosαcosβ的方程组，通过解方程获解.