题目内容
设{an}是公比大于1的等比数列,Sn为数列{an}的前n项和.已知S3=7,且a1+3,3a2,a3+4构成等差数列.(1)求数列{an}的通项公式.
(2)令bn=lna3n+1,n=1,2,…,求数列{bn}的前n项和Tn.
【答案】分析:(1)由{an}是公比大于1的等比数列,S3=7,且a1+3,3a2,a3+4构成等差数列,我们不难构造方程组,解方程组即可求出相关基本量,进而给出数列{an}的通项公式.
(2)由bn=lna3n+1,n=1,2,…,我们易给出数列{bn}的通项公式,分析后可得:数列{bn}是一个等差数列,代入等差数列前n项和公式即可求出Tn
解答:解:(1)由已知得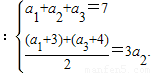
解得a2=2.
设数列{an}的公比为q,由a2=2,
可得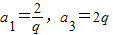 .
.
又S3=7,可知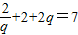 ,
,
即2q2-5q+2=0,
解得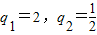
由题意得q>1,
∴q=2
∴a1=1.故数列{an}的通项为an=2n-1.
(2)由于bn=lna3n+1,n=1,2,
由(1)得a3n+1=23n
∴bn=ln23n=3nln2又bn+1-bn=3ln2n
∴{bn}是等差数列.
∴Tn=b1+b2++bn
=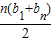
=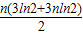
=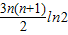 .
.
故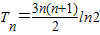 .
.
点评:解答特殊数列(等差数列与等比数列)的问题时,根据已知条件构造关于基本量的方程,解方程求出基本量,再根据定义确定数列的通项公式及前n项和公式,然后代入进行运算.
(2)由bn=lna3n+1,n=1,2,…,我们易给出数列{bn}的通项公式,分析后可得:数列{bn}是一个等差数列,代入等差数列前n项和公式即可求出Tn
解答:解:(1)由已知得
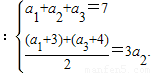
解得a2=2.
设数列{an}的公比为q,由a2=2,
可得
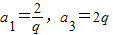 .
.又S3=7,可知
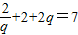 ,
,即2q2-5q+2=0,
解得
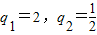
由题意得q>1,
∴q=2
∴a1=1.故数列{an}的通项为an=2n-1.
(2)由于bn=lna3n+1,n=1,2,
由(1)得a3n+1=23n
∴bn=ln23n=3nln2又bn+1-bn=3ln2n
∴{bn}是等差数列.
∴Tn=b1+b2++bn
=
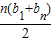
=
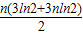
=
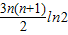 .
.故
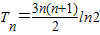 .
.点评:解答特殊数列(等差数列与等比数列)的问题时,根据已知条件构造关于基本量的方程,解方程求出基本量,再根据定义确定数列的通项公式及前n项和公式,然后代入进行运算.

练习册系列答案
相关题目