题目内容
定义方程f = f
= f
 的实数根
的实数根 叫做函数的“新驻点”,若函数g
叫做函数的“新驻点”,若函数g =x,
=x,
h =ln(x+1),
=ln(x+1),
 =
= 的“新驻点”分别为
的“新驻点”分别为 ,
, ,
, ,则的大小关系为 ( )
,则的大小关系为 ( )
A. > > > > | B. > >  > > | C. > > > > | D. > > > > |
C
解析试题分析:∵g′(x)=1,h′(x)= ,φ′(x)=-sinx,由题意得:
,φ′(x)=-sinx,由题意得:
α=1,ln(β+1)= ,cosγ=-sinγ,①∵ln(β+1)=
,cosγ=-sinγ,①∵ln(β+1)= ,∴
,∴ ,当β≥1时,β+1≥2,∴β+1≤
,当β≥1时,β+1≥2,∴β+1≤ <2,∴β<1,这与β≥1矛盾,∴0<β<1;
<2,∴β<1,这与β≥1矛盾,∴0<β<1;
②∵cosγ=-sinγ,∴γ>1.∴γ>α>β.
考点:本题考查了导数的运用
点评:函数、导数、不等式密不可分,此题就是一个典型的代表,其中对对数方程和三次方程根的范围的讨论是一个难点

练习册系列答案
相关题目
已知函数 与
与 轴切于
轴切于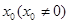 点,且极小值为
点,且极小值为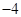 ,则
,则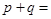 ( )
( )
| A.12 | B.13 | C.15 | D.16 |
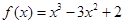 在区间
在区间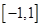 上的最大值是( )
上的最大值是( )
| A.-2 | B.0 | C.2 | D.4 |
由直线 ,曲线
,曲线 及
及 轴所围图形的面积为( )
轴所围图形的面积为( )
A. | B.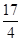 | C. | D. |
定积分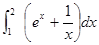 的值为 ( )
的值为 ( )
A. | B. |
C.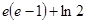 | D.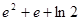 |
若函数 的导函数
的导函数 ,则使得函数
,则使得函数 单调递减的一个充分不必要条件是
单调递减的一个充分不必要条件是 ( )
( )
| A.(0,1) | B.[0,2] | C.(2,3) | D.(2,4) |
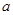 、
、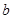 ,则集合
,则集合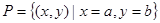 所表示的平面图形面积等于( )
所表示的平面图形面积等于( )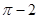
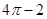
 在点(1,1)处的切线与
在点(1,1)处的切线与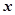 轴及直线
轴及直线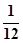
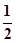


 是
是 的导函数,
的导函数,