题目内容
定积分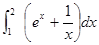 的值为 ( )
的值为 ( )
A. | B. |
C.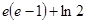 | D.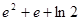 |
C
解析试题分析:根据已知条件,找到原函数,结合微积分基本定理可知 =
=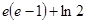 ,故可知选C
,故可知选C
考点:定积分的运用
点评:解决该试题的关键是利用微积分基本定理,求解运算,属于基础题。

练习册系列答案
相关题目
如果 为偶函数,且
为偶函数,且 导数存在,则
导数存在,则 的值为( )
的值为( )
| A.0 | B.1 | C.2 | D. |
由直线 ,曲线
,曲线 及
及 轴所围成的图形的面积为( )
轴所围成的图形的面积为( )
A. | B. | C. | D. |
定义方程f = f
= f
 的实数根
的实数根 叫做函数的“新驻点”,若函数g
叫做函数的“新驻点”,若函数g =x,
=x,
h =ln(x+1),
=ln(x+1),
 =
= 的“新驻点”分别为
的“新驻点”分别为 ,
, ,
, ,则的大小关系为 ( )
,则的大小关系为 ( )
A. > > > > | B. > >  > > | C. > > > > | D. > > > > |
 =( )
=( )
A. | B.2 | C. | D. |
已知函数 在
在 上满足
上满足  ,则曲线
,则曲线 在
在 处的切线方程是
处的切线方程是
A. | B. | C. | D. |
对于R上可导的任意函数f(x),若满足(x-1) ³0,则必有( )
³0,则必有( )
| A.f(0)+f(2)<2f(1) | B.f(0)+f(2)£2f(1) |
| C.f(0)+f(2)³2f(1) | D.f(0)+f(2)>2f(1) |
设函数 ,当
,当 时,
时, 恒成立,则实数
恒成立,则实数 的取值范围是
的取值范围是
A. | B. | C. | D. |
函数 图象如图,则函数
图象如图,则函数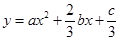 的单调递增区间为( )
的单调递增区间为( )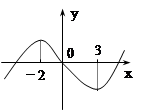
A.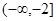 | B.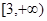 | C.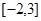 | D. |