题目内容
已知钝角△ABC的最长边为2,其余两边的长为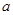 、
、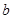 ,则集合
,则集合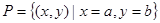 所表示的平面图形面积等于( )
所表示的平面图形面积等于( )
| A.2 | B.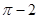 | C.4 | D.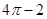 |
B
解析试题分析:由钝角三角形ABC的最长边的长为2,其余两边长为a、b,由余弦定理可得 <4,再由两边之和大于第三边,得a+b>2,且a>0,b>0,点P表示的范围如下图所示,
<4,再由两边之和大于第三边,得a+b>2,且a>0,b>0,点P表示的范围如下图所示, 由图可得可行域的面积为π-2,故选B
由图可得可行域的面积为π-2,故选B
考点:本题考查了线性规划的运用
点评:对于此类问题根据已知结合余弦定理及钝角三角形的性质特征求出约束条件是解答的关键

练习册系列答案
相关题目
如图是导函数 的图象,则下列命题错误的是( )
的图象,则下列命题错误的是( )
A.导函数 在 在 处有极小值 处有极小值 |
B.导函数 在 在 处有极大值 处有极大值 |
C.函数 在 在 处有极小值 处有极小值 |
D.函数 在 在 处有极小值 处有极小值 |
已知函数 的导函数
的导函数 的图象如图所示,则关于函数
的图象如图所示,则关于函数 ,下列说法正确的是
,下列说法正确的是
A.在 处取得极大值 处取得极大值 |
B.在区间 上是增函数 上是增函数 |
C.在 处取得极大值 处取得极大值 |
D.在区间 上是减函数 上是减函数 |
由直线 ,曲线
,曲线 及
及 轴所围成的图形的面积为( )
轴所围成的图形的面积为( )
A. | B. | C. | D. |
已知函数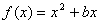 的图像在点
的图像在点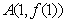 处的切线的斜率为3,数列
处的切线的斜率为3,数列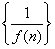 的前
的前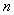 项和为
项和为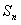 ,则
,则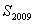 的值为( )
的值为( )
A.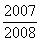 | B.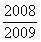 | C.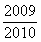 | D.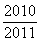 |
定义方程f = f
= f
 的实数根
的实数根 叫做函数的“新驻点”,若函数g
叫做函数的“新驻点”,若函数g =x,
=x,
h =ln(x+1),
=ln(x+1),
 =
= 的“新驻点”分别为
的“新驻点”分别为 ,
, ,
, ,则的大小关系为 ( )
,则的大小关系为 ( )
A. > > > > | B. > >  > > | C. > > > > | D. > > > > |
 =( )
=( )
A. | B.2 | C. | D. |
对于R上可导的任意函数f(x),若满足(x-1) ³0,则必有( )
³0,则必有( )
| A.f(0)+f(2)<2f(1) | B.f(0)+f(2)£2f(1) |
| C.f(0)+f(2)³2f(1) | D.f(0)+f(2)>2f(1) |
已知 ,则( )
,则( )
A. | B. | C. | D.以上都有可能 |