题目内容
设函数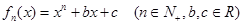
(1)设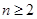 ,
,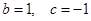 ,证明:
,证明: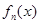 在区间
在区间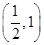 内存在唯一的零点;
内存在唯一的零点;
(2) 设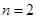 ,若对任意
,若对任意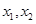
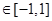 ,有
,有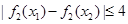 ,求
,求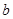 的取值范围;
的取值范围;
(3)在(1)的条件下,设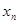 是
是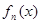 在
在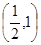 内的零点,判断数列
内的零点,判断数列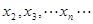 的增减性.
的增减性.
【答案】
(1) 见解析;(2)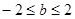 ;(3)见解析.
;(3)见解析.
【解析】
试题分析:(1) 先根据零点存在性定理判断在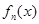 在
在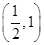 内存在零点,在利用导数说明函数在
内存在零点,在利用导数说明函数在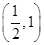 上是单调递增的,从而说明
上是单调递增的,从而说明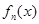 在区间
在区间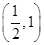 内存在唯一的零点;(2)此问可用两种解法:第一种,当
内存在唯一的零点;(2)此问可用两种解法:第一种,当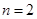 时,
时,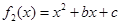 ,根据题意判断出
,根据题意判断出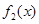 在
在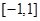 上最大值与最小值之差
上最大值与最小值之差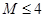 ,据此分类讨论如下:(ⅰ)当
,据此分类讨论如下:(ⅰ)当 ;(ⅱ)当
;(ⅱ)当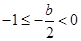 ;(ⅲ)当
;(ⅲ)当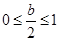 ,综上可知,
,综上可知, 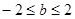 ;第二种,用
;第二种,用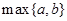 表示
表示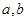 中的较大者,直接代入计算即可;(3)先设出零点
中的较大者,直接代入计算即可;(3)先设出零点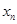 ,然后根据
,然后根据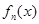 在
在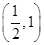 上是递增的得出结论.
上是递增的得出结论.
试题解析:(1)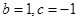 ,
,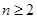 时,
时,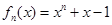
∵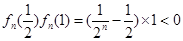 ,∴
,∴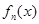 在
在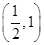 内存在零点. 又当
内存在零点. 又当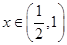 时,
时,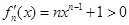 ,∴
,∴
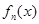 在
在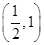 上是单调递增的,所以
上是单调递增的,所以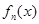 在
在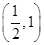 内存在唯一零点.
内存在唯一零点.
(2)当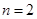 时,
时,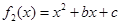 ,对任意
,对任意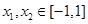 都有
都有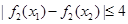 等价于
等价于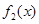 在
在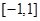 上最大值与最小值之差
上最大值与最小值之差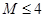 ,据此分类讨论如下:(ⅰ)当
,据此分类讨论如下:(ⅰ)当 ,即
,即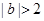 时,
时, 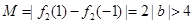 ,与题设矛盾
,与题设矛盾
(ⅱ)当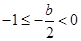 ,即
,即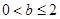 时,
时, 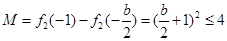 恒成立
恒成立
(ⅲ)当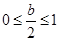 ,即
,即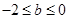 时,
时, 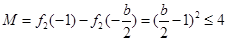 恒成立.
恒成立.
综上可知, 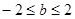
注:(ⅱ)(ⅲ)也可合并证明如下:
用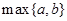 表示
表示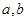 中的较大者.当
中的较大者.当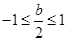 ,即
,即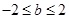 时,
时,

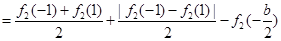
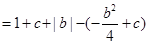
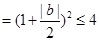 恒成立 .
恒成立 .
(3)证法一 设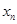 是
是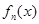 在
在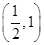 内的唯一零点
内的唯一零点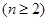
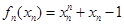 ,
,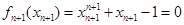 ,
,
于是有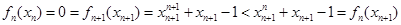
又由(1)知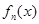 在
在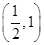 上是递增的,故
上是递增的,故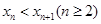 , 所以,数列
, 所以,数列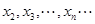 是递增数列.
是递增数列.
证法二 设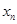 是
是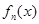 在
在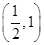 内的唯一零点
内的唯一零点
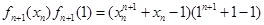
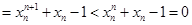 则
则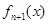 的零点
的零点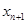 在
在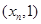 内,故
内,故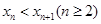 ,
,
所以,数列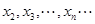 是递增数列.
是递增数列.
考点:1.零点存在性定理;2.利用导数判断函数单调性;3.利用函数单调性判断大小.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
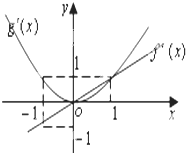 已知函数f′(x),g′(x)分别是二次函数f(x)和三次函数g(x)的导函数,它们在同一坐标系下的图象如图所示,设函数h(x)=f(x)-g(x),则( )
已知函数f′(x),g′(x)分别是二次函数f(x)和三次函数g(x)的导函数,它们在同一坐标系下的图象如图所示,设函数h(x)=f(x)-g(x),则( )