题目内容
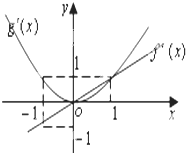已知函数f′（x），g′（x）分别是二次函数f（x）和三次函数g（x）的导函数，它们在同一坐标系下的图象如图所示，设函数h（x）=f（x）-g（x），则（ ）分析：求出函数h（x）=f（x）-g（x）的解析式，然后将-1，0，1代入比较即可求出h（-1），h（0），h（1）的大小关系．
解答：解：二次函数f（x）的导函数是一次函数，三次函数g（x）的导函数是二次函数
∵一次函数过点（0，0），（1，1），
∴f'（x）=x，
∴f（x）=
x2+C，
∵二次函数过点（1，1），（-1，1），（0，0），
∴g'（x）=x2，
∴g（x）=
x3+C'，
∴h（x）=f（x）-g（x）=
x2-
x3+C-C'
记C-C'=m为常数
则h（-1）=
+m，h（0）=m，h（1）=
+m
∴h（0）＜h（1）＜h（-1）．
故选D．
∵一次函数过点（0，0），（1，1），
∴f'（x）=x，
∴f（x）=
| 1 |
| 2 |
∵二次函数过点（1，1），（-1，1），（0，0），
∴g'（x）=x2，
∴g（x）=
| 1 |
| 3 |
∴h（x）=f（x）-g（x）=
| 1 |
| 2 |
| 1 |
| 3 |
记C-C'=m为常数
则h（-1）=
| 5 |
| 6 |
| 1 |
| 6 |
∴h（0）＜h（1）＜h（-1）．
故选D．
点评：本题主要考查根据导函数求原函数，考查比较函数值大小，搞清导函数与原函数之间的关系是解题的关键，属于中档题．
练习册系列答案
相关题目
已知函数f（x）=x2-bx的图象在点A（1，f（1））处的切线l与直线3x-y+2=0平行，若数列{
}的前n项和为Sn，则S2010的值为（ ）
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|