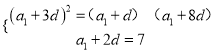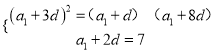题目内容
【题目】已知函数![]() (
(![]() ,且
,且![]() ),且
),且![]() .
.
(1)求实数![]() 的值;
的值;
(2)判断函数![]() 的奇偶性并证明
的奇偶性并证明
(3)若函数![]() 有零点,求实数
有零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)2(2)奇函数.见解析 (3)![]() 或
或![]() .
.
【解析】
(1)代入![]() 求解即可.
求解即可.
(2)由(1)化简可得![]() ,再分析
,再分析![]() 与
与![]() 的关系判定即可.
的关系判定即可.
(3)分析可知![]() 有实根,再换元令
有实根,再换元令![]() ,分析
,分析![]() ,
,![]() 的取值范围进而求得
的取值范围进而求得![]() 的取值范围即可.
的取值范围即可.
(1)因为![]()
解得![]()
(2)![]() 是奇函数.
是奇函数.
由![]() 得:
得:![]()
故![]() ,所以
,所以![]() 是奇函数
是奇函数
(3)方法一:
代入![]() 可得
可得![]()
因为![]() 有零点,所以
有零点,所以![]() 有实根.
有实根.
显然![]() 不是
不是![]() 的实根,所以
的实根,所以![]() 有实根.
有实根.
设![]() ,
,![]() ,
,![]() .因为
.因为![]() .
.
①当![]() 时,
时,![]() ,所以
,所以![]() ,
,
所以![]()
②当![]() 时,
时,![]() ,
,
所以![]()
综上,![]() 的值域为
的值域为![]()
所以,当![]() 时,
时,![]() 有实根,
有实根,
即![]() 有零点
有零点
方法二:代入![]() 可得
可得![]()
因为![]() 有零点,所以
有零点,所以![]() 有实根.
有实根.
所以![]() 有实根.
有实根.
显然,![]() 时上式不成立,所以
时上式不成立,所以![]() 有实根
有实根
因为![]() ,
,
所以![]()
所以![]() 或
或![]() .
.
所以,当![]() 时,
时,![]() 有实根.
有实根.
即![]() 有零点
有零点

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某企业生产甲、乙两种产品均需要![]() ,
,![]() 两种原料,已知生产1吨每种产品所需原料及每天原料的可用限额如表所示.如果生产1吨甲、乙产品可获得利润分别为3万元、4万元,则该企业每天可获得最大利润为( )
两种原料,已知生产1吨每种产品所需原料及每天原料的可用限额如表所示.如果生产1吨甲、乙产品可获得利润分别为3万元、4万元,则该企业每天可获得最大利润为( )
甲 | 乙 | 原料限额 | |
| 3 | 2 | 10 |
| 1 | 2 | 6 |
A. 10万元B. 12万元C. 13万元D. 14万元