题目内容
关于x方程|x+
|-|x-
|-kx-1=0的不相等的实数根最多有 .
| 1 |
| x |
| 1 |
| x |
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:将方程转化为函数,作出函数的图象,利用数形结合即可得到结论.
解答:
 解:由程|x+
解:由程|x+
|-|x-
|-kx-1=0得程|x+
|-|x-
|=kx+1,
设f(x)=|x+
|-|x-
|,
则f(x)=
,作出函数f(x)的图象如图:
函数g(x)=kx+1过定点(0,1),
则由图象可知,函数f(x)和g(x)的图象最多有四个交点,
故关于x方程|x+
|-|x-
|-kx-1=0的不相等的实数根最多有4个,
故答案为:4
 解:由程|x+
解:由程|x+| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
设f(x)=|x+
| 1 |
| x |
| 1 |
| x |
则f(x)=
|
函数g(x)=kx+1过定点(0,1),
则由图象可知,函数f(x)和g(x)的图象最多有四个交点,
故关于x方程|x+
| 1 |
| x |
| 1 |
| x |
故答案为:4
点评:本题主要考查函数和方程之间的关系,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
已知AB∥PQ,BC∥QR,∠ABC=60°,则∠PQR等于( )
| A、60° |
| B、60°或120° |
| C、120° |
| D、以上结论都不对 |
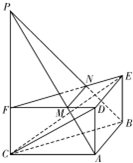 如图,在正三棱柱ABC-DEF中,AB=2,AD=1.P是CF的沿长线上一点,FP=t.过A,B,P三点的平面交FD于M,交FE于N.
如图,在正三棱柱ABC-DEF中,AB=2,AD=1.P是CF的沿长线上一点,FP=t.过A,B,P三点的平面交FD于M,交FE于N.