题目内容
设
是定义在R上的可导函数,当x≠0时,
,则关于x的函数
的零点个数为( )
是定义在R上的可导函数,当x≠0时,,则关于x的函数的零点个数为( )| A．l | B．2 | C．0 | D．0或 2 |
C
试题分析：由
，得
，当
时，
，即
，函数
单调递增；当
时，
，即
，函数单调递减．又
，函数
的零点个数等价为函数
的零点个数．当
时，
，当时，，所以函数无零点，所以函数
的零点个数为0个．故选C．
练习册系列答案
相关题目
，
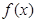的单调区间；
有且只有一个解，求实数m的取值范围；
且
，
时，若有
，求证：
.
.
.的单调区间；
的极值.
.
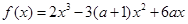
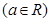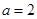时，求函数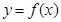
的单调区间；
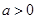时，函数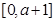
上的最大值为
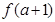，求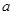
的取值范围.
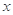亿元，其中用于风景区改造为
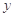亿元。该市决定建立生态环境改造投资方案，该方案要求同时具备下列三个条件：①每年用于风景区改造费用
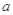亿元，至多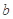
亿元；③每年用于风景区改造费用
，
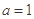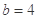，请你分析能否采用函数模型y＝
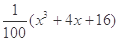作为生态环境改造投资方案.
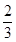x＋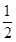
，h(x)＝
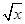，设F(x)＝f(x)－h(x)，求F(x)的单调区间与极值．
，g(x)＝x2－2ax＋4，若任意x1∈[0,1]，存在x2∈[1,2]，使f(x1)≥g(x2)，则实数a的取值范围是______．
的单调增区间是 ．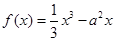
满足：对于任意的
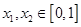，都有
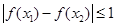恒成立，则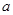
的取值范围是（ ）
