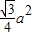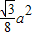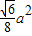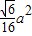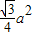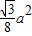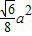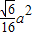Question

正△ABC的边长为a,AD⊥BD,D为垂足,沿AD将△ABD折起,使∠BDC=90°,则折后点B到直线AC的距离等于__________.

Answer 1

答案:a

解析:如图所示,折前的边AB,∠BDA折起后都不变,则折起后的△ABC是等腰三角形.

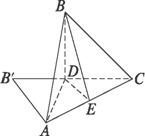
∵∠BDA=90°,

∴BD⊥AD.

又∵∠BDC=90°,

∴BD⊥DC.

又AD∩DC=D,

∴BD⊥平面ADC.

过D作DE⊥AC于E点,连结BE,则AC⊥BE,

即BE为B点到直线AC的距离.

在Rt△ADC中,AD=a(原△ABC中的高),

DC=a,AC=a,∴DE=.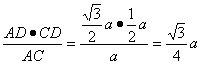

在Rt△BDE中,BD=a,DE=a,∴BE=a.