题目内容
已知正△ABC的边长为a,那么△ABC的平面直观图△A′B′C′的面积为( )A.
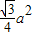
B.
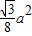
C.
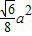
D.
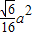
【答案】分析:由正△ABC的边长为a,知正△ABC的高为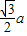 ,画到平面直观图△A′B′C′后,“高”变成原来的一半,且与底面夹角45度,故△A′B′C′的高为
,画到平面直观图△A′B′C′后,“高”变成原来的一半,且与底面夹角45度,故△A′B′C′的高为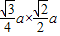 =
=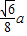 ,由此能求出△A′B′C′的面积.
,由此能求出△A′B′C′的面积.
解答:解:∵正△ABC的边长为a,∴正△ABC的高为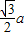 ,
,
画到平面直观图△A′B′C′后,“高”变成原来的一半,且与底面夹角45度,
∴△A′B′C′的高为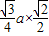 =
=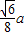 ,
,
∴△A′B′C′的面积S=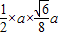 =
=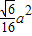 .
.
故选D.
点评:本题考查平面图形的直观图的性质和应用,解题时要认真审题,仔细解答,注意合理地进行等价转化.
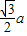 ,画到平面直观图△A′B′C′后,“高”变成原来的一半,且与底面夹角45度,故△A′B′C′的高为
,画到平面直观图△A′B′C′后,“高”变成原来的一半,且与底面夹角45度,故△A′B′C′的高为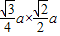 =
=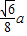 ,由此能求出△A′B′C′的面积.
,由此能求出△A′B′C′的面积.解答:解:∵正△ABC的边长为a,∴正△ABC的高为
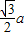 ,
,画到平面直观图△A′B′C′后,“高”变成原来的一半,且与底面夹角45度,
∴△A′B′C′的高为
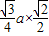 =
=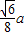 ,
,∴△A′B′C′的面积S=
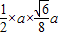 =
=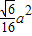 .
.故选D.
点评:本题考查平面图形的直观图的性质和应用,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
已知正△ABC的边长为
,则到三个顶点的距离都为1的平面有( )
4
| ||
| 3 |
| A、1个 | B、3个 | C、5个 | D、7个 |