题目内容
已知函数
（
）.
(I)若
的定义域和值域均是
，求实数
的值；
(II)若在区间
上是减函数，且对任意的
，
，总有
，求实数的取值范围.
(I) a=2， (II) 
.
解析试题分析：(I)研究二次函数性质，关键研究对称轴与定义区间之间相对位置关系. 因为函数f(x)对称轴为x=a,抛物线开口向上，在 （1，a）上单调递减，则f(1)=a,f(a)=1,代入
解得a=2， (II) 因为在区间上是减函数，所以
因此
，所以1离开对称轴的距离最远，所以在区间
最大值应为
，最小值应为
，因此对任意的，，总有，就可化为
，
，解得
，又
所以
（1）因为函数f(x)对称轴为x=a,抛物线开口向上，在 （1，a）上单调递减，
则f(1)=a,f(a)=1,代入解得a=2 -6分
（2）可得
，显然在区间最大值应为，最小值应为
所以，解得 -14分
考点：二次函数最值
练习册系列答案
相关题目
中，
为奇数，
均为整数，且
均为奇数.求证：
无整数根。
+2.
．现已知相距18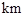
的A，B两家化工厂（污染源）的污染强度分别为
，它们连线上任意一点C处的污染指数
等于两化工厂对该处的污染指数之和．设
（
的函数； （2）若
，且
时，
的值．
（
）
有3个不同的根，求实数
的取值范围；
在
上恰有两个极值点
，且满足
，若存在，求实数
.
，讨论函数
在区间
上的单调性；
且
，对任意的
，试比较
的大小．
时，求
的极大值点；
的图象
与函数
的图象
交于
、
两点，过线段
的中点做
轴的垂线分别交
、
，证明：
.
，求
的解析式；
在
上恒成立，求实数
的取值范围.