题目内容
已知函数f(x)=aln x= (a为常数
(a为常数 ).
).
(1)若曲线y=f(x)在点(1,f(1))处的切线与直线x+2y-5=0垂直,求a的值;
(2)求函数f(x)的单调区间;
(3)当x≥1时,f(x)≤2x-3恒成立,求a的取值范围.
解 (1)函数f(x)的定义域为{x|x>0},f′(x)=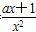 .
.
又曲线y=f(x)在 点(1,f(1))处的切线与直线x+2y-5=0垂直,
点(1,f(1))处的切线与直线x+2y-5=0垂直,
所以f′(1)=a+1=2,即a=1.(4分)
(2)由f′(x)=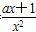 (x>0),
(x>0),
当a≥0时,
f′(x)>0恒成立,所以f(x)的单调增区间为(0,+∞).
当a<0时,
由f′(x)>0,得0<x<-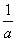 ,
,
所以f(x)的单调增区间为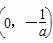 ;
;
由f′(x)<0,得x>-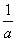 ,
,
所以f(x)的单调减区间为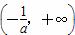
(3)设g(x)=aln x- -2x+3,x∈[1,+∞),
-2x+3,x∈[1,+∞),
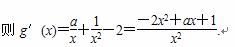 令h(x)=-2x2+ax+1,考虑到h(0)=1>0,
令h(x)=-2x2+ax+1,考虑到h(0)=1>0,
当a≤1时,
h(x)=- 2x2+ax+1的对称轴x=
2x2+ax+1的对称轴x=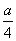 <1,
<1,
h(x)在[1,+∞)上是减函数,h(x)≤h(1)=a-1≤0,
所以g′(x)≤0,g(x)在[1,+∞)上是减函数,
所以g(x)≤ g(1)=0,即f(x)≤2x2-3恒成立.
g(1)=0,即f(x)≤2x2-3恒成立.
当a>1时,
令h(x)=-2x2+ax+1=0,
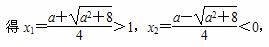 当x∈[1,x1)时,h(x)>0,即g′(x)>0,
当x∈[1,x1)时,h(x)>0,即g′(x)>0,
g(x)在[1,x1)上是增函数;
当x∈(x1,+∞)时,h(x)<0,即g′(x)<0,
g(x)在(x1,+∞)上是减函数.
所以0=g(1)<g(x1),即f(x1)>2x1-3,不满足题意.
综上,a的取值范围为a≤1.(16分)

练习册系列答案
相关题目
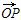 =xe1+ye2,则将有序实数对(x,y)叫做向量
=xe1+ye2,则将有序实数对(x,y)叫做向量
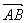 =a,
=a, =b,试用a、b分别表示
=b,试用a、b分别表示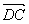 、
、 、
、 。
。
 满足条件
满足条件 (k为常数),若
(k为常数),若 的最大值为8,则k=_________.
的最大值为8,则k=_________.
 的极值;
的极值; 时,函数
时,函数 的最大值为
的最大值为 ?若存在,求实数a的取值范围,若不存在,请说明理由.
?若存在,求实数a的取值范围,若不存在,请说明理由. 椭圆C:
椭圆C: (a>b>0)上任一点P到两个焦点的距离的和为2
(a>b>0)上任一点P到两个焦点的距离的和为2 ,P与椭圆长轴两顶点连线的斜率之积为-
,P与椭圆长轴两顶点连线的斜率之积为- .设直线l过椭圆C的右焦点F,交椭圆C于两点A(x1,y1),B(x2,y2).
.设直线l过椭圆C的右焦点F,交椭圆C于两点A(x1,y1),B(x2,y2).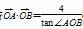 (O为坐标原点),求|y1-y2|的值;
(O为坐标原点),求|y1-y2|的值;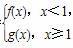 若P是曲线y=F(x)上异于原点O的任意一点,在曲线y=F(x)上总存在另一点Q,使得△POQ中的∠POQ为钝角,且PQ的中点在y轴上,求a的取值范围.
若P是曲线y=F(x)上异于原点O的任意一点,在曲线y=F(x)上总存在另一点Q,使得△POQ中的∠POQ为钝角,且PQ的中点在y轴上,求a的取值范围.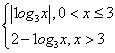 ,若a,b,c互不相等,且f(a)=f(b)=f(c),则a+b+c的取值范围为( )
,若a,b,c互不相等,且f(a)=f(b)=f(c),则a+b+c的取值范围为( )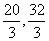 ) B.(
) B.( ) C.(
) C.(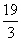 ,12) D.(6,l2)
,12) D.(6,l2) 、
、 的坐标满足不等式组
的坐标满足不等式组 ,若
,若 ,则
,则 的取值范围是
的取值范围是 B.
B.  C.
C.  D.
D. 