题目内容
11．以线段两个端点（3，8）和（7，4）为直径的圆的方程（x-5）2+（y-6）2=8．分析 根据题意，分析可得要求的圆的圆心是点A（3，8）和B（7，4）的中点，其半径为线段AB长度的一半，分别求出圆心坐标以及半径，即可得答案．
解答 解：根据题意，设A的坐标为（3，8），B的坐标为（7，4）
要求的圆的圆心是点A（3，8）和B（7，4）的中点，
则其圆心的坐标为（$\frac{3+7}{2}$，$\frac{8+4}{2}$），即（5，6）；
其半径为线段AB长度的一半，即r=$\frac{1}{2}$$\sqrt{（3-7）^{2}+（8-4）^{2}}$=2$\sqrt{2}$，
则要求圆的方程为（x-5）2+（y-6）2=（2$\sqrt{2}$）2，
即（x-5）2+（y-6）2=8，
故答案为：（x-5）2+（y-6）2=8．
点评 本题考查圆的标准方程的求法，求圆的标准方程的关键是找到圆心的坐标以及半径．
练习册系列答案
阅读快车系列答案
相关题目
16．某几何体的三视图如图所示，则该几何体的体积为（ ）
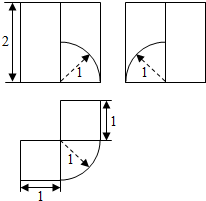
| A． | 6+$\frac{π}{8}$ | B． | 6+$\frac{π}{6}$ | C． | 4+$\frac{π}{8}$ | D． | 4+$\frac{π}{6}$ |
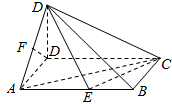如图，四边形ABCD为矩形，DD1⊥底面ABCD，AD=DD1=$\frac{1}{2}$AB，点F为AD1的中点．点E在棱AB上移动．
12．
如图，F1，F2分别是双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a\;，\;b＞0）$的左、右两焦点，B是虚轴的端点，直线F1B与C的两条渐近线分别交于P，Q两点，线段PQ的垂直平分线与x轴交于点M．若|MF2|=|F1F2|，则C的离心率是（ ）
如图，F1，F2分别是双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a\;，\;b＞0）$的左、右两焦点，B是虚轴的端点，直线F1B与C的两条渐近线分别交于P，Q两点，线段PQ的垂直平分线与x轴交于点M．若|MF2|=|F1F2|，则C的离心率是（ ）| A． | $\frac{2\sqrt{3}}{3}$ | B． | $\frac{\sqrt{6}}{2}$ | C． | $\sqrt{2}$ | D． | $\sqrt{3}$ |