题目内容
(本小题满分12分)
如图,ABCD为梯形,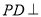 平面ABCD,AB//CD,
平面ABCD,AB//CD,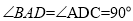
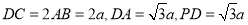 ,E为BC中点
,E为BC中点
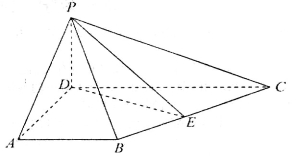
(I)求证:平面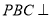 平面PDE;
平面PDE;
(II)线段PC上是否存在一点F,使PA//平面BDF?若有,请找出具体位置,并进行证明;若无,请分析说明理由.
(1)见解析;(2)见解析
【解析】
试题分析:(1)证明两个平面垂直,首先考虑直线与平面垂直,也可以简单记为“证面面垂直,找线面垂直”,是化归思想的体现,这种思想方法与空间中的平行关系的证明类似,掌握化归与转化思想方法是解决这类题的关键;(2) 连结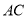 ,
, 相交于点
相交于点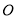 ,根据
,根据 可得
可得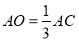 ,然后结合直线与平面平行的判定定理可知在线段
,然后结合直线与平面平行的判定定理可知在线段 上存在一点
上存在一点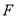 ,使得
,使得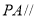 平面
平面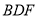 .
.
试题解析:证明:(Ⅰ) 连结

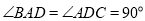 ,
,
所以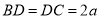 ,
,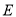 为
为 中点
中点
所以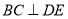 3分
3分
又因为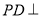 平面
平面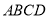 ,
,
所以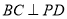
因为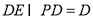 4分
4分
所以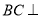 平面
平面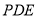 5分
5分
因为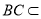 平面
平面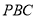 ,所以平面
,所以平面 平面
平面 6分
6分
(Ⅱ)当点 位于
位于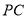 三分之一分点(靠近
三分之一分点(靠近 点)时,
点)时, 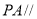 平面
平面 7分
7分
连结 交于
交于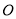 点,
点,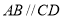 ,所以
,所以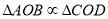

所以 中,
中,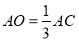 10分
10分
而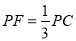
所以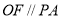 11分
11分
而 平面
平面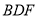
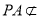 平面
平面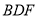
所以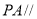 平面
平面 12分
12分
考点:空间几何的位置关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
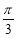 ,a+b与b的夹角为
,a+b与b的夹角为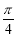 ,则
,则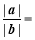 ( )
( )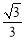 (B)
(B)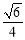
 (D)
(D)
 ,
, __________.
__________. 为纯虚数,则实数
为纯虚数,则实数
 B.
B.  C.2 D.
C.2 D. 
 与双曲线
与双曲线 有公共的焦点
有公共的焦点 ,则双曲线的渐近线方程为________.
,则双曲线的渐近线方程为________.
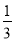 C.
C.  D.
D. 
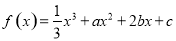 有两个极值点
有两个极值点 ,则直线
,则直线 的斜率的取值范围是
的斜率的取值范围是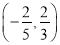 B.
B. 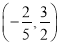 C.
C.  D.
D. 
 的图像向左平移个
的图像向左平移个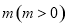 单位长度后,所得的图像关于
单位长度后,所得的图像关于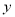 轴对称,则
轴对称,则 的最小值是
的最小值是