题目内容
17.①命题“存在${x_0}∈R,{2^{x_0}}≤0$”的否定是“不存在${x_0}∈R,{2^{x_0}}>0$”②若z是纯虚数,则z2<0
③若x+y≠3,则x≠2或y≠1
④以直角三角形的一边为旋转轴,旋转一周所得的旋转体是圆锥
以上正确命题的序号是②③.
分析 写出原命题的否定,可判断①;根据虚数单位的定义,可判断②;判断原命题的逆否命题的真假,可判断③;根据圆锥的几何特征,可判断④.
解答 解:①命题“存在${x_0}∈R,{2^{x_0}}≤0$”的否定是“?${x_0}∈R,{2^{x_0}}>0$”,故为假命题;
②若z是纯虚数,不妨令z=bi(b≠0),则z2=-b2<0,故为真命题;
③若x+y≠3,则x≠2或y≠1的逆否命题为:若x=2且y=1,则x+y=3为真命题,故原命题也为真命题;
④以直角三角形的直角边为旋转轴,旋转一周所得的旋转体才是圆锥,故为假命题;
故答案为:②③
点评 本题考查的知识点是特称命题,算数,四种命题,圆锥的几何特征,难度中档.

练习册系列答案
相关题目
7.威力实施“爱的教育”实践活动,宇华教育集团决定举行“爱在宇华”教师演讲比赛.焦作校区决定从高中部、初中部、小学部和幼教部这四个部门选出12人组成代表队代表焦作校区参赛,选手来源如下表:
焦作校区选手经过出色表现获得冠军,现要从中选出两名选手代表冠军队发言.
(1)求这两名队员来自同一部门的概率;
(2)设选出的两名选手中来自高中部的人数为ξ,求随机变量ξ的分布列及数学期望Eξ.
| 部门 | 高中部 | 初中部 | 小学部 | 幼教部 |
| 人数 | 4 | 4 | 2 | 2 |
(1)求这两名队员来自同一部门的概率;
(2)设选出的两名选手中来自高中部的人数为ξ,求随机变量ξ的分布列及数学期望Eξ.
6.设a=log36,b=log510,c=log612,则( )
| A. | a>b>c | B. | a>c>b | C. | b>c>a | D. | c>b>a |


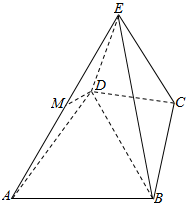 如图几何体E-ABCD是四棱锥,△ABD为正三角形,∠BCD=120°,CB=CD=CE=1,AB=AD=AE=$\sqrt{3}$,且EC⊥BD.
如图几何体E-ABCD是四棱锥,△ABD为正三角形,∠BCD=120°,CB=CD=CE=1,AB=AD=AE=$\sqrt{3}$,且EC⊥BD.