题目内容
设等差数列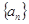 的首项为1,其前n项和为
的首项为1,其前n项和为 ,
,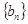 是公比为正整数的等比数列,其首项为3,前n项和为
是公比为正整数的等比数列,其首项为3,前n项和为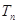 . 若
. 若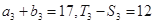 .
.
(1)求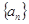 ,
,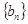 的通项公式;(7分)
的通项公式;(7分)
(2)求数列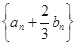 的前n项和
的前n项和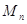 .(5分)
.(5分)
(1) (2)
(2)
解析试题分析:解:(1)设等差数列 的公差为d,等比数列
的公差为d,等比数列 的公比为q
的公比为q
由已知


考点:数列的通项公式和求和
点评:解决的关键是利用等差数列和等比数列的通项公式来得到通项公式,并利用分组求和得到结论,属于基础题。

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
题目内容
设等差数列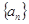 的首项为1,其前n项和为
的首项为1,其前n项和为 ,
,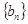 是公比为正整数的等比数列,其首项为3,前n项和为
是公比为正整数的等比数列,其首项为3,前n项和为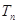 . 若
. 若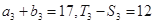 .
.
(1)求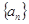 ,
,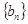 的通项公式;(7分)
的通项公式;(7分)
(2)求数列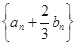 的前n项和
的前n项和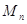 .(5分)
.(5分)
(1) (2)
(2)
解析试题分析:解:(1)设等差数列 的公差为d,等比数列
的公差为d,等比数列 的公比为q
的公比为q
由已知


考点:数列的通项公式和求和
点评:解决的关键是利用等差数列和等比数列的通项公式来得到通项公式,并利用分组求和得到结论,属于基础题。

 春雨教育同步作文系列答案
春雨教育同步作文系列答案