题目内容
10.若函数f(x)=x2+ax+2是R上的偶函数,其中常数a∈R,则函数y=$\frac{f(x)}{x}$(x>0)的最小值为2$\sqrt{2}$.分析 利用偶函数求出a,然后利用基本不等式求解最小值即可.
解答 解:函数f(x)=x2+ax+2是R上的偶函数,可知a=0,
又x>0
函数y=$\frac{f(x)}{x}$=x+$\frac{2}{x}$≥2$\sqrt{x•\frac{2}{x}}$=2$\sqrt{2}$,当且仅当x=$\sqrt{2}$时取等号.
故答案为:2$\sqrt{2}$.
点评 本题考查二次函数的性质,基本不等式在最值中的应用,考查计算能力.

练习册系列答案
相关题目
5.抛物线x=-$\frac{1}{4}$y2的焦点坐标是( )
| A. | (-1,0) | B. | (0,-1) | C. | (-$\frac{1}{16}$,0) | D. | (0,-$\frac{1}{16}$) |
2.哈三中某兴趣小组为了调查高中生的数学成绩是否与物理成绩有关系,在高二年级随机调查了50名学生,调查结果表明:在数学成绩较好的25人中有18人物理成绩好,另外7人物理成绩一般;在数学成绩一般的25人中有6人物理成绩好,另外19人物理成绩一般.
(Ⅰ) 试根据以上数据完成以下2×2列联表,并运用独立性检验思想,指出是否有99.9%把握认为高中生的数学成绩与物理成绩有关系.
(Ⅱ) 现将4名数学成绩好且物理成绩也好的学生分别编号为1,2,3,4,将4名数学成绩好但物理成绩一般的学生也分别编号1,2,3,4,从这两组学生中各任选1人进行学习交流,求被选取的2名学生编号之和不大于5的概率.
附:
${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$.
(Ⅰ) 试根据以上数据完成以下2×2列联表,并运用独立性检验思想,指出是否有99.9%把握认为高中生的数学成绩与物理成绩有关系.
| 数学成绩好 | 数学成绩一般 | 总计 | |
| 物理成绩好 | |||
| 物理成绩一般 | |||
| 总计 |
附:
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
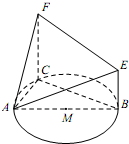 如图,某简单几何体的一个面ABC内接于圆M,AB是圆M的直径,CF∥BE,BE⊥平面ABC,且AB=2,AC=1,BE+CF=7.
如图,某简单几何体的一个面ABC内接于圆M,AB是圆M的直径,CF∥BE,BE⊥平面ABC,且AB=2,AC=1,BE+CF=7.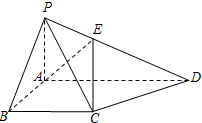 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,∠ABC=∠BAD=90°,且PA=AB=BC=$\frac{1}{2}$AD=1,PA⊥平面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,∠ABC=∠BAD=90°,且PA=AB=BC=$\frac{1}{2}$AD=1,PA⊥平面ABCD.