题目内容
已知c为正实数,数列{an}满足a1=1,an+1=(1)证明![]() ≤an≤1(n∈N*);
≤an≤1(n∈N*);
(2)t是满足t=![]() 的正实数,记bn=|an-t|(n∈N*),数列{bn}的前n项和为Sn.证明Sn≤|tn-1|(n∈N*);
的正实数,记bn=|an-t|(n∈N*),数列{bn}的前n项和为Sn.证明Sn≤|tn-1|(n∈N*);
(3)若c=![]() ,记dn=
,记dn=![]() (n∈N*),求数列{dn}的前n项和Tn.
(n∈N*),求数列{dn}的前n项和Tn.
(1)证明:①当n=1时,∵c>0,a1=1,∴![]() ≤a1≤1.
≤a1≤1.
②假设n=k时,有![]() ≤ak≤1,
≤ak≤1,
则![]() +c≤ak+c≤1+c,∴
+c≤ak+c≤1+c,∴![]() ≤
≤![]() ≤
≤![]() ≤1,即n=k+1时不等式也成立.
≤1,即n=k+1时不等式也成立.
∴![]() ≤an≤1(n∈N*).
≤an≤1(n∈N*).
(2)证明:由t=![]() ,c>0,可得t≠1,
,c>0,可得t≠1,
由an+1=![]() ,t=
,t=![]() ,得an+1-t=
,得an+1-t=![]() -
-![]() =
=![]() (n∈N*),
(n∈N*),
∴|an+1-t|=![]() =tan+1|an-t|≤t|an-t|≤t2|an-1-t|≤…≤tn|1-t|(n∈N*).
=tan+1|an-t|≤t|an-t|≤t2|an-1-t|≤…≤tn|1-t|(n∈N*).
又|a1-t|=|1-t|,
∴|an-t|≤tn-1|1-t|(n∈N*).
∴Sn≤|1-t|(1+t+t2+…+tn-1)=|tn-1|.
(3)解:∵c=![]() ,∴an+1=
,∴an+1=![]() .∴an+1+2=
.∴an+1+2=![]() +2=
+2= .
.
∴![]() .
.
∴dn+1=![]() +
+![]() (n∈N*).∴dn+1
(n∈N*).∴dn+1![]() =
=![]() (dn
(dn![]() )(n∈N*).
)(n∈N*).
∴{dn![]() }是首项为d1
}是首项为d1![]() =
=![]() ,公比为
,公比为![]() 的等比数列.
的等比数列.
∴dn![]() =
=![]() (
(![]() )n-1,即dn=
)n-1,即dn=![]() (
(![]() )n-1(n∈N*).
)n-1(n∈N*).
∴Tn=![]() +
+![]() (
(![]() )n(n∈N*).
)n(n∈N*).

练习册系列答案
相关题目
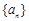 由
由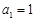 ,
,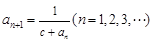 确定.
确定.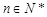 ,证明:
,证明: ;
;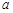 是满足
是满足 的正实数,且
的正实数,且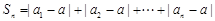 ,
, .
.