题目内容
已知C为正实数,数列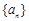 由
由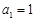 ,
,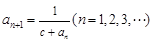 确定.
确定.
(Ⅰ)对于一切的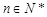 ,证明:
,证明: ;
;
(Ⅱ)若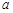 是满足
是满足 的正实数,且
的正实数,且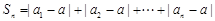 ,
,
证明: .
.
【答案】
(Ⅰ)用数学归纳法证明:见解析;. (Ⅱ)见解析。
【解析】(I)用数学归纳法证明:第一步:先验证:当n=1时,不等式成立;
第二步:先假设n=k时,结论成立,再证明当n=k+1时,不等式也成立.在证明时,一定要用上n=k时的归纳假设.
(II) 解决本小题的关键是根据 ,
,
从而可得 .
.
(Ⅰ)用数学归纳法证明:当 时,
时, ,
, ,
, 成立.
成立.
假设 时结论成立,即
时结论成立,即 ,则
,则 ,即
,即 .
.
∴ ,∴
,∴ 时结论也成立,综上,对一切的
时结论也成立,综上,对一切的 ,
, 成立. (Ⅱ)
成立. (Ⅱ) ,
,
∴ .当
.当 时,
时, ,与
,与 矛盾,故
矛盾,故 . ∴
. ∴
 =
= =1-
=1-
<1

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目