Question

如图，已知三棱锥O﹣ABC的侧棱OA，OB，OC两两垂直，且OA=1，OB=OC=2，E是OC的中点．
（1）求异面直线BE与AC所成角的余弦值；
（2）求二面角A﹣BE﹣C的余弦值．

Answer 1

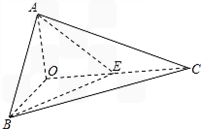
解：（1）以O为原点，OB，OC，OA分别为x，y，z轴建立空间直角坐标系．
则有A（0，0，1），B（2，0，0），C（0，2，0），E（0，1，0）．
=（2，0，0）﹣（0，1，0）=（2，﹣1，0），
=（0，2，﹣1），
cos＜＞=．
由于异面直线BE与AC所成的角是锐角，故其余弦值是．
（2）=（0，1，﹣1），
设平面ABE的法向量为m₁=（x，y，z），则由m₁⊥，m_1⊥，得
取n=（1，2，2），
平面BEC的一个法向量为n₂=（0，0，1），
cos＜n₁．n₂＞==
由于二面角A﹣BE﹣C的平面角是n₁与n₂的夹角的补角，其余弦值是﹣.