题目内容
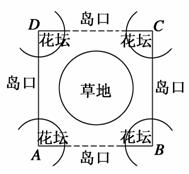
如图，现要在边长为100 m的正方形ABCD内建一个交通“环岛”．以正方形的四个顶点为圆心在四个角分别建半径为x m(x不小于9)的扇形花坛，以正方形的中心为圆心建一个半径为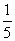
x2 m的圆形草地．为了保证道路畅通，岛口宽不小于60 m，绕岛行驶的路宽均不小于10 m.
(1)求x的取值范围；(运算中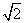
取1.4)
(2)若中间草地的造价为a元/m2，四个花坛的造价为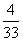
ax元/m2，其余区域的造价为
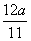元/m2，当x取何值时，可使“环岛”的整体造价最低？
解 (1)由题意，得
解得
即9≤x≤15.
(2)记“环岛”的整体造价为y元，则由题意，得
令f(x)＝－
x4＋
x3－12x2，
则f′(x)＝－
x3＋4x2－24x
＝
由f′(x)＝0，解得x＝10或x＝15.
列表如下：
∴当x＝10，f(x)取极小值，即y取最小值．
故当x＝10 m时，可使“环岛”的整体造价最低．
练习册系列答案
相关题目
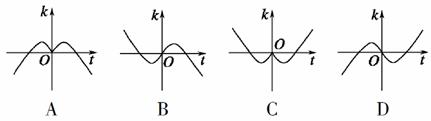
，则( )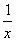
(x∈(－∞，0)∪(0，＋∞))的图象为C1，C1关于点A(2,1)的对称的图象为C2，C2对应的函数为g(x)．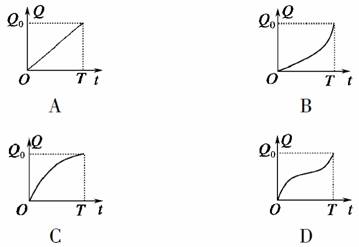
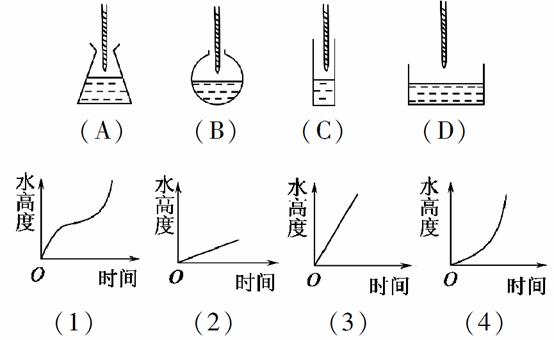
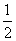x2＋4x－3lnx在[t，t＋1]上不单调，则t的取值范围是________．
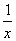＋2x＋2e2x，直线x＝1，x＝e和x轴所围成的区域的面积是________．