题目内容
13.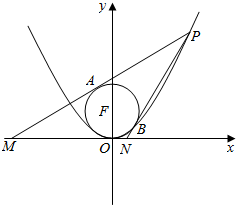 (文科)如图,已知抛物线C:y=$\frac{1}{4}$x2,点P(x0,y0)为抛物线上一点,y0∈[3,5],圆F方程为x2+(y-1)2=1,过点P作圆F的两条切线PA,PB分别交x轴于点M,N,切点分别为A,B.
(文科)如图,已知抛物线C:y=$\frac{1}{4}$x2,点P(x0,y0)为抛物线上一点,y0∈[3,5],圆F方程为x2+(y-1)2=1,过点P作圆F的两条切线PA,PB分别交x轴于点M,N,切点分别为A,B.①求四边形PAFB面积的最大值.
②求线段MN长度的最大值.
分析 ①四边形PAFB面积S=2S△APF=2$•\frac{1}{2}•|AP|$,求出|AP|的最大值,即可求四边形PAFB面积的最大值.
②求出M,N的坐标,表示出|MN|,即可求线段MN长度的最大值.
解答 解:①设P(x0,$\frac{1}{4}$x02),则$\frac{1}{4}$x02∈[3,5],x02∈[12,20],
由题意,∠FAP=90°,∠FBP=90°,
△AFP中,|AP|=$\sqrt{|PF{|}^{2}-|AF{|}^{2}}$=$\frac{\sqrt{{{x}_{0}}^{4}+8{{x}_{0}}^{2}}}{4}$,
令x02=t∈[12,20],则|AP|=$\frac{1}{4}$$\sqrt{{t}^{2}+8t}$,
四边形PAFB面积S=2S△APF=2$•\frac{1}{2}•|AP|$=$\frac{1}{4}$$\sqrt{{t}^{2}+8t}$,
最大值为$\sqrt{35}$,此时x02=20,即y0=5时取到;
②设P(x0,$\frac{1}{4}$x02),则圆的切线方程为y-$\frac{1}{4}$x02=k(x-x0).
由点到直线的距离公式可得$\frac{|k{x}_{0}+1-\frac{1}{4}{{x}_{0}}^{2}|}{\sqrt{{k}^{2}+1}}$=1
∴(x02-1)k+2x0(1-$\frac{1}{4}$x02)k+(1-$\frac{1}{4}$x02)2-1=0,
设两根为k1,k2,则k1+k2=-$\frac{2{x}_{0}(1-\frac{1}{4}{{x}_{0}}^{2})}{{{x}_{0}}^{2}-1}$,k1k2=$\frac{(1-\frac{1}{4}{{x}_{0}}^{2})^{2}-1}{{{x}_{0}}^{2}-1}$,
∵M(x0-$\frac{1}{4{k}_{1}}$x02,0),N(x0-$\frac{1}{4{k}_{2}}$x02,0),
∴|MN|=$\frac{1}{4}$x02|$\frac{1}{{k}_{1}}$-$\frac{1}{{k}_{2}}$|=2•$\frac{\sqrt{{t}^{2}+8t}}{t-8}$(x02=t∈[12,20],t-8=m∈[4,12])
∴|MN|=2•$\frac{\sqrt{{n}^{2}+24n+128}}{n}$,
令$\frac{1}{n}$=p∈[$\frac{1}{12}$,$\frac{1}{4}$],
∴|MN|=2$\sqrt{128{p}^{2}+24p+1}$,最大值为2$\sqrt{15}$,p=$\frac{1}{4}$,即y0=3时取到.
点评 本题考查圆锥曲线的综合,考查四边形面积的计算,考查韦达定理的运用,考查学生分析解决问题的能力,属于中档题.

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案| A. | 相离 | B. | 相切 | C. | 相交 | D. | 以上都有可能 |
| A. | x2+y2+3x+6y=0 | B. | x2+y2-3x+6y=0 | C. | x2+y2+3x-6y=0 | D. | x2+y2-3x-6y=0 |
| A. | 命题“若x≠1,则x2-3x+2≠0”的逆否命题是“若x2-3x+2=0则x=1”. | |
| B. | 若p∧q为真命题,则p∨q为真命题. | |
| C. | 若命题p:?x∈R,x2+x+1≠0,则¬p:?x∈R,x2+x+1=0. | |
| D. | “x>2”是“x2-3x+2>0”成立的必要不充分条件. |
| A. | |a|>$\sqrt{2}$ | B. | $\sqrt{2}$<|a|<$\sqrt{3}$ | C. | |a|>$\sqrt{3}$ | D. | |a|<3 |