题目内容
2.已知全集U=R,集合A={x|x2-3x≤0},B={x|a≤x≤a+2,a∈R}(1)当a=1时,求A∩B;
(2)当集合A,B满足B?A时,求实数a的取值范围.
分析 (1)由x2-3x≤0,解出可得A.当a=1时,B=[1,3].即可得出A∩B.
(2)由B?A,可得$\left\{\begin{array}{l}{a≥0}\\{a+2≤3}\end{array}\right.$,解出即可得出.
解答 解:(1)由x2-3x≤0,解得0≤x≤3,∴A=[0,3].
当a=1时,B=[1,3].
∴A∩B=[1,3].
(2)∵B?A,
∴$\left\{\begin{array}{l}{a≥0}\\{a+2≤3}\end{array}\right.$,解得0≤a≤1,
∴实数a的取值范围是[0,1].
点评 本题考查了一元二次不等式的解法、集合之间的关系及其运算性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
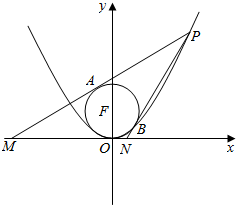 (文科)如图,已知抛物线C:y=$\frac{1}{4}$x2,点P(x0,y0)为抛物线上一点,y0∈[3,5],圆F方程为x2+(y-1)2=1,过点P作圆F的两条切线PA,PB分别交x轴于点M,N,切点分别为A,B.
(文科)如图,已知抛物线C:y=$\frac{1}{4}$x2,点P(x0,y0)为抛物线上一点,y0∈[3,5],圆F方程为x2+(y-1)2=1,过点P作圆F的两条切线PA,PB分别交x轴于点M,N,切点分别为A,B.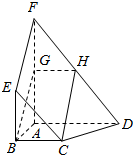 如图,平面ABEF⊥平面ABCD,四边形ABEF与ABCD都是直角梯形,∠BAD=∠FAB=90°,BC∥AD且BC=$\frac{1}{2}$AD,BE∥AF且BE=$\frac{1}{2}$AF,G,H分别为FA,FD的中点.证明:四边形BCHG是平行四边形.
如图,平面ABEF⊥平面ABCD,四边形ABEF与ABCD都是直角梯形,∠BAD=∠FAB=90°,BC∥AD且BC=$\frac{1}{2}$AD,BE∥AF且BE=$\frac{1}{2}$AF,G,H分别为FA,FD的中点.证明:四边形BCHG是平行四边形.