题目内容
12.已知数列{an}的前n项和Sn,对任意n∈N*,Sn=(-1)nan+$\frac{1}{2^n}$+n-3且(an+1-p)(an-p)<0恒成立,则实数p的取值范围是$({-\frac{3}{4},\frac{11}{4}})$.分析 由数列递推式求出首项,写出n≥2时的递推式,作差后对n分偶数和奇数讨论,求出数列通项公式,可得函数${a}_{n}=\frac{1}{{2}^{n+1}}-1$(n为正奇数)为减函数,最大值为${a}_{1}=-\frac{3}{4}$,函数${a}_{n}=3-\frac{1}{{2}^{n}}$(n为正偶数)为增函数,最小值为${a}_{2}=\frac{11}{4}$.再由(an+1-p)(an-p)<0恒成立求得实数p的取值范围.
解答 解:由${S_n}={(-1)^n}{a_n}+\frac{1}{2^n}+n-3$,得${a}_{1}=-\frac{3}{4}$;
当n≥2时,an=Sn-Sn-1=$(-1)^{n}{a}_{n}+\frac{1}{{2}^{n}}+n-3-(-1)^{n-1}{a}_{n-1}-\frac{1}{{2}^{n-1}}-(n-1)+3$
=$(-1)^{n}{a}_{n}+(-1)^{n}{a}_{n-1}-\frac{1}{{2}^{n}}+1$.
若n为偶数,则${a}_{n-1}=\frac{1}{{2}^{n}}-1$,∴${a}_{n}=\frac{1}{{2}^{n+1}}-1$(n为正奇数);
若n为奇数,则${a}_{n-1}=-2{a}_{n}-\frac{1}{{2}^{n}}+1$=$-2(\frac{1}{{2}^{n+1}}-1)-\frac{1}{{2}^{n}}+1$=$3-\frac{1}{{2}^{n-1}}$,
∴${a}_{n}=3-\frac{1}{{2}^{n}}$(n为正偶数).
函数${a}_{n}=\frac{1}{{2}^{n+1}}-1$(n为正奇数)为减函数,最大值为${a}_{1}=-\frac{3}{4}$,
函数${a}_{n}=3-\frac{1}{{2}^{n}}$(n为正偶数)为增函数,最小值为${a}_{2}=\frac{11}{4}$.
若(an+1-p)(an-p)<0恒成立,
则a1<p<a2,即$-\frac{3}{4}<p<\frac{11}{4}$.
故答案为:$({-\frac{3}{4},\frac{11}{4}})$.
点评 本题考查数列递推式,考查了数列通项公式的求法,体现了分类讨论的数学思想方法和数学转化思想方法,是中档题.

| A. | a+1>b | B. | 2a>2b | C. | a2>b2 | D. | lga>lgb |
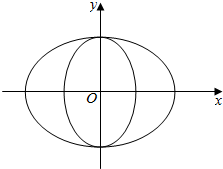 如图,曲线Γ由两个椭圆T1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$和椭圆T2:$\frac{y^2}{b^2}+\frac{x^2}{c^2}=1({b>c>0})$组成,当a,b,c成等比数列时,称曲线Γ为“猫眼曲线”.
如图,曲线Γ由两个椭圆T1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$和椭圆T2:$\frac{y^2}{b^2}+\frac{x^2}{c^2}=1({b>c>0})$组成,当a,b,c成等比数列时,称曲线Γ为“猫眼曲线”.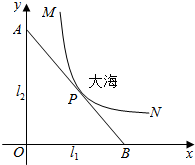 某沿海城市的海边有两条相互垂直的直线型公路l1、l2,海岸边界MPN近似地看成一条曲线段.为开发旅游资源,需修建一条连接两条公路的直线型观光大道AB,且直线AB与曲线MPN有且仅有一个公共点P(即直线与曲线相切),如图所示.若曲线段MPN是函数$y=\frac{a}{x}$图象的一段,点M到l1、l2的距离分别为8千米和1千米,点N到l2的距离为10千米,以l1、l2分别为x、y轴建立如图所示的平面直角坐标系xOy,设点P的横坐标为p.
某沿海城市的海边有两条相互垂直的直线型公路l1、l2,海岸边界MPN近似地看成一条曲线段.为开发旅游资源,需修建一条连接两条公路的直线型观光大道AB,且直线AB与曲线MPN有且仅有一个公共点P(即直线与曲线相切),如图所示.若曲线段MPN是函数$y=\frac{a}{x}$图象的一段,点M到l1、l2的距离分别为8千米和1千米,点N到l2的距离为10千米,以l1、l2分别为x、y轴建立如图所示的平面直角坐标系xOy,设点P的横坐标为p. 如图,在直角梯形ABCD中,∠BAD=∠ADC=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD=2a.
如图,在直角梯形ABCD中,∠BAD=∠ADC=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD=2a.