题目内容
若点P在抛物线y=3x2+4x+2上，A(0，-3)、B(-1，-1)使△ABP的面积最小，则P点的坐标是( )A．(-
，
) B.(-
) C.(-1,1) D.(0,2)
C
解析：本题主要考查曲线上的点到曲线外一直线的最短距离求解，其通法就是将直线平移与曲线相切则切点到直线的距离即为最短距离；据题意知要使三角形面积最小，只需曲线上的点到直线AB的距离最小即可，易知kAB=-2，设与直线AB平行的直线与曲线切于点(x0，y0)，即=6x+=6x0+4=-2x0=-1故切点坐标为(-1，1).
练习册系列答案
阅读快车系列答案
相关题目
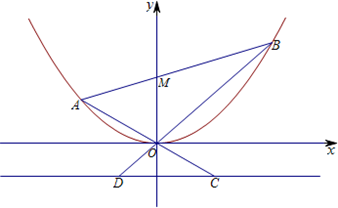已知抛物线E：x2=4y，直线l过点M（0，2）且与抛物线交于A、B两点，直线OA、OB分别与抛物线的准线l0交于C、D．