Question

已知△ABC的顶点B、C的坐标分别为(－1,－3)、(3,5),若点A在抛物线y=x²－4上移动,求△ABC的重心P的轨迹.

Answer 1

解:设△ABC的重心P的坐标为(x,y),顶点A的坐标为(x₁,y₁),则y₁=x₁²－4.

由重心坐标公式得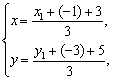

∴代入y₁=x₁²－4得3y－2=(3x－2)²－4,化简整理得y=3x²－4x＋.

又直线BC的方程为=,即y=2x－1,

由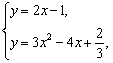

得或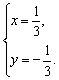

而A、B、C三点不在同一直线上,

∴P、B、C三点不共线,

即轨迹中应去掉点(,)和(,－).

故△ABC的重心P的轨迹为开口向上的抛物线y=3x²－4x＋,但不包括点(,)和(,－).

点评:(1)动点P与A有关系,用P的坐标表示A的坐标,并代入A的轨迹方程得到P的轨迹方程.这种求方程的方法称作相关点法.

(2)求动点的轨迹与求轨迹方程的要求不同,前者是求轨迹图形.