题目内容
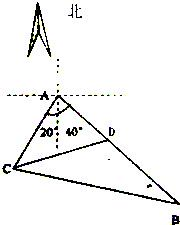 某观测站C在城A的南偏西20°的方向上.由A城出发有一条公路AB,走向为南偏东40°.由C处测得距C为31公里的B处有一辆车正沿公路向A城驶去,该车行驶了20公里到达D处,此时C,D之间距离为21公里.问这辆车还需行驶多少公里才能到达A城?
某观测站C在城A的南偏西20°的方向上.由A城出发有一条公路AB,走向为南偏东40°.由C处测得距C为31公里的B处有一辆车正沿公路向A城驶去,该车行驶了20公里到达D处,此时C,D之间距离为21公里.问这辆车还需行驶多少公里才能到达A城?
分析:根据题意可知CD,BC,BD在△BCD中,由余弦定理求得cos∠BDC,进而设∠ADC=α,则sinα,cosα可求,在△ACD中,由正弦定理求得得AD,答案可得.
解答:解:由已知得CD=21,BC=31,BD=20,
在△BCD中,由余弦定理得cos∠BDC=
=-
.
设∠ADC=α,则cosα=
,sinα=
,
在△ACD中,由正弦定理得
=
,
AD=
sin(
+α)=
(
×
+
×
)=15,
即所求的距离为15公里.
在△BCD中,由余弦定理得cos∠BDC=
| 212+202-312 |
| 2×21×20 |
| 1 |
| 7 |
设∠ADC=α,则cosα=
| 1 |
| 7 |
4
| ||
| 7 |
在△ACD中,由正弦定理得
| AD | ||
sin(
|
| 21 | ||
sin
|
AD=
| 42 | ||
|
| π |
| 3 |
| 42 | ||
|
| ||
| 2 |
| 1 |
| 7 |
| 1 |
| 2 |
4
| ||
| 7 |
即所求的距离为15公里.
点评:本题主要考查了解三角新的实际应用.解题的关键是利用正弦定理,利用边和角的关系求得答案.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目
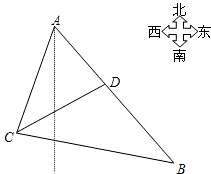 某观测站C在城A的南20°西的方向上,由A城出发有一条公路,走向是南40°东,在C处测得距C为31千米的公路上B处,有一人正沿公路向A城走去,走了20千米后,到达D处,此时C、D间距离为21千米,问这人还需走多少千米到达A城?
某观测站C在城A的南20°西的方向上,由A城出发有一条公路,走向是南40°东,在C处测得距C为31千米的公路上B处,有一人正沿公路向A城走去,走了20千米后,到达D处,此时C、D间距离为21千米,问这人还需走多少千米到达A城?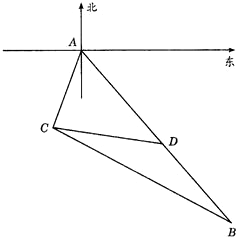 如图,某观测站C在城A的南偏西20°方向上,从城A出发有一条公路,走向是南偏东40°,在C处测得距离C处31千米的公路上的B处有一辆正沿着公路向城A驶去,行驶了20千米后到达D处,测得C、D二处间距离为21千米,这时此车距城A多少千米?
如图,某观测站C在城A的南偏西20°方向上,从城A出发有一条公路,走向是南偏东40°,在C处测得距离C处31千米的公路上的B处有一辆正沿着公路向城A驶去,行驶了20千米后到达D处,测得C、D二处间距离为21千米,这时此车距城A多少千米? 某观测站C在城A的南偏西20°方向上,从城A出发有一条公路,走向是南偏东40°,在距C处31公里的公路上的B处有一个人正沿着公路向城A走去,走20公里后到达D处,测得CD=21公里,求这时此人距城A多少公里?某同学甲已经由余弦定理求得cos∠CDB=-
某观测站C在城A的南偏西20°方向上,从城A出发有一条公路,走向是南偏东40°,在距C处31公里的公路上的B处有一个人正沿着公路向城A走去,走20公里后到达D处,测得CD=21公里,求这时此人距城A多少公里?某同学甲已经由余弦定理求得cos∠CDB=-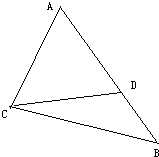 某观测站C在城A的南偏西15°方向,从城A出发有一条公路,走向是南偏东30°,在C处测得距C处7km的公路上B处有一辆汽车正沿着公路向A城开去,开3km后,到达D处,测得CD=5km.
某观测站C在城A的南偏西15°方向,从城A出发有一条公路,走向是南偏东30°,在C处测得距C处7km的公路上B处有一辆汽车正沿着公路向A城开去,开3km后,到达D处,测得CD=5km.